��Ŀ����
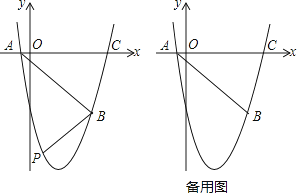
����Ŀ����ƽ��ֱ������ϵ�У���֪������y=x2+bx+c�Ķ���M������Ϊ����1����4��������x�ύ�ڵ�A����B����A�ڵ�B����ߣ�����y�ύ�ڵ�C��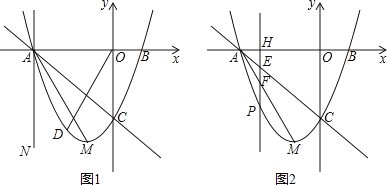
��1����գ�b= �� c= �� ֱ��AC�Ľ���ʽΪ
��2��ֱ��x=t��x���ཻ�ڵ�H��
�ٵ�t=��3ʱ�õ�ֱ��AN����ͼ1������DΪֱ��AC�·���������һ�㣬����COD=��MAN�������ʱ��D�����ꣻ
�ڵ���3��t����1ʱ����ͼ2����ֱ��x=t���߶�AC��AM�������߷ֱ��ཻ�ڵ�E��F��P����֤���߶�HE��EF��FP������ɵ��������Σ�����˵��������εǵ�����ֵΪ ![]() �����ʱt��ֵ��
�����ʱt��ֵ��
���𰸡�
��1��2����3��y=��x��3
��2��
�⣺�����D������Ϊ��m��m2+2m��3����
�ߡ�COD=��MAN��
��tan��COD=tan��MAN��
�� ![]() =
= ![]() ��
��
��ã�m=�� ![]() ��
��
�ߩ�3��m��0��
��m=�� ![]() ��
��
�ʵ�D������Ϊ���� ![]() ����2
����2 ![]() ����
����
����ֱ��AM�Ľ���ʽΪy=mx+n��
����A����3��0����M����1����4�����룬
�ã� ![]() ����ã�
����ã� ![]() ��
��
��ֱ��AM�Ľ���ʽΪ��y=��2x��6��
�ߵ�x=tʱ��HE=������t��3��=t+3��HF=������2t��6��=2t+6��HP=����t2+2t��3����
��HE=EF=HF��HE=t+3��FP=��t2��4t��3��
��HE+EF��FP=2��t+3��+t2+4t+3=��t+3��2��0��
��HE+EF��FP��
��HE+FP��EF��EF+FP��HE��
�൱��3��t����1ʱ���߶�HE��EF��FP������ɵ��������Σ�
������ã� ![]() =
= ![]() ����
���� ![]() =
= ![]() ��
��
�����ã�5t2+26t+33=0��
��ã�t1=��3��t2=�� ![]() ��
��
�ߩ�3��t����1��
��t=�� ![]() ��
��
���������⣺��1����������y=x2+bx+c�Ķ���M������Ϊ����1����4����
�� 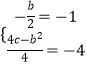 ����ã�
����ã� ![]() ��
��
�������߽���ʽΪ��y=x2+2x��3��
��y=0���ã�x2+2x��3=0����ã�x1=1��x2=��3��
��A����3��0����B��1��0����
��x=0����y=��3��
��C��0����3����
��ֱ��AC�Ľ���ʽΪ��y=kx+b��
��A����3��0����C��0����3�����룬
�ã� ![]() ����ã�
����ã� ![]() ��
��
��ֱ��AC�Ľ���ʽΪ��y=��x��3��
���Դ��ǣ�2����3��y=��x��3��