Question

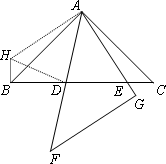
如图1，在同一平面内，将两个全等的等腰直角三角形ABC和AFG摆放在一起，A为公共顶点，∠BAC＝∠AGF＝90°，它们的斜边长为2，若?ABC固定不动，△AFG绕点A旋转，AF、AG与边BC的交点分别为D、E(点D不与点B重合，点E不与点C重合)，设BE＝m，CD＝n．

(1)请在图中找出两对相似而不全等的三角形，并选取其中一对进行证明．

(2)求m与n的函数关系式，直接写出自变量n的取值范围．

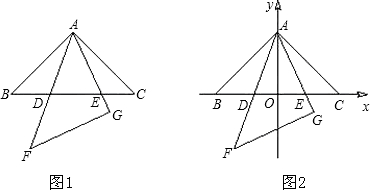
(3)以?ABC的斜边BC所在的直线为x轴，BC边上的高所在的直线为y轴，建立平面直角坐标系(如图2)．在边BC上找一点D，使BD＝CE，求出D点的坐标，并通过计算验证BD²＋CE²＝DE²．

(4)在旋转过程中，(3)中的等量关系BD²＋CE²＝DE²是否始终成立，若成立，请证明，若不成立，请说明理由．

Answer 1

答案：
解析：

解：(1)△ABE∽△DAE，△ABE∽△DCA　　1分 　　∵∠BAE＝∠BAD＋45°，∠CDA＝∠BAD＋45° 　　∴∠BAE＝∠CDA 　　又∠B＝∠C＝45° 　　∴△ABE∽△DCA　　3分 　　(2)∵△ABE∽△DCA 　　∴ 　　由依题意可知CA＝BA＝ 　　∴ 　　∴m＝　　5分 　　自变量n的取值范围为1＜n＜2　　6分 　　(3)由BD＝CE可得BE＝CD，即m＝n 　　∵m＝ 　　∴m＝n＝ 　　∵OB＝OC＝BC＝1 　　∴OE＝OD＝－1 　　∴D(1－，0)　　7分 　　∴BD＝OB－OD＝1－(－1)＝2－＝CE，DE＝BC－2BD＝2－2(2－)＝2－2 　　∵BD＋CE＝2BD＝2(2－)＝12－8，DE＝(2－2)＝12－8 　　∴BD＋CE＝DE　　8分 　　(4)成立　　9分 　　证明：如图，将?ACE绕点A顺时针旋转90°至?ABH的位置，则CE＝HB，AE＝AH， 　　∠ABH＝∠C＝45°，旋转角∠EAH＝90°． 　　连接HD，在△EAD和△HAD中 　　∵AE＝AH，∠HAD＝∠EAH－∠FAG＝45°＝∠EAD，AD＝AD． 　　∴△EAD≌△HAD 　　∴DH＝DE 　　又∠HBD＝∠ABH＋∠ABD＝90° 　　∴BD＋HB＝DH 　　即BD＋CE＝DE　　12分