题目内容
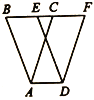
【题目】如图,在□ABCD中,O是对角线AC的中点,过O作AC的垂线与边AD、BC分别交于E、F。
(1)求证:四边形AFCE是菱形;
(2)若AF⊥BC,试猜想四边形AFCE是什么特殊四边形,并说明理由。

【答案】(1)证明见解析(2)正方形
【解析】
(1)根据平行四边形性质推出AD∥BC,根据平行线分线段成比例定理求出OE=OF,推出平行四边形AFCE,根据菱形的判定推出即可;
(2)由“有一个直角的菱形是正方形”判定四边形AFCE是正方形.
∵平行四边形ABCD,
∴AD∥BC,
∴![]() ,
,
∵O是对角线AC的中点,
∴AO=OC,
∴OE=OF,
∴四边形AFCE是平行四边形,
∵EF⊥AC,
∴平行四边形AFCE是菱形;
(2)四边形AFCE为正方形.
∵∠AFC=90°,由(1)知四边形AFCE为菱形,
∴四边形AFCE是正方形(有一个直角的菱形是正方形).

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目