题目内容
如图,AB为⊙O的直径,D是⊙O上的一点,过O点作AB的垂线交AD于点E,交BD的延长线于点C,F为CE上一点,且FD=FE.(1)请探究FD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为2,BD=
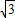 ,求BC的长.
,求BC的长.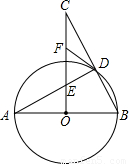
【答案】分析:(1)连接圆心和切点,利用OC⊥AB可证得∠ODF=90°,从而得到其位置关系;
(2)易证得△COB∽△ADB,利用相似比求解即可.
解答: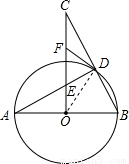 解:(1)FD与⊙O相切.1分
解:(1)FD与⊙O相切.1分
证明:连接OD;
∵FE=FD,
∴∠FED=∠FDE; 3分
又∵OA=OD,
∴∠OAD=∠ODA,
∵∠OEA+∠OAE=90°,∠FED=∠AEO,
∴∠ODE+∠FDE=90°,
∴FD与⊙O相切.
(2)∵AB为⊙O的直径,
∴∠ADB=90°;
∵OC⊥AB,
∴∠COB=∠ADB=90°,∠CBO=∠ABD,
∴△COB∽△ADB,
∴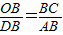 ,
,
∴BC=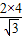 =
=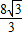 .
.
点评:求直线和圆的位置关系,首先要猜想是相切,那么应连接圆心和切点,证半径和直线所夹的角是90°,需注意利用相似来求相关线段的长度.
(2)易证得△COB∽△ADB,利用相似比求解即可.
解答:
 解:(1)FD与⊙O相切.1分
解:(1)FD与⊙O相切.1分证明:连接OD;
∵FE=FD,
∴∠FED=∠FDE; 3分
又∵OA=OD,
∴∠OAD=∠ODA,
∵∠OEA+∠OAE=90°,∠FED=∠AEO,
∴∠ODE+∠FDE=90°,
∴FD与⊙O相切.
(2)∵AB为⊙O的直径,
∴∠ADB=90°;
∵OC⊥AB,
∴∠COB=∠ADB=90°,∠CBO=∠ABD,
∴△COB∽△ADB,
∴
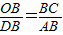 ,
,∴BC=
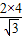 =
=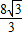 .
.点评:求直线和圆的位置关系,首先要猜想是相切,那么应连接圆心和切点,证半径和直线所夹的角是90°,需注意利用相似来求相关线段的长度.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为( )
如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为( )| A、1cm | B、2cm | C、3cm | D、4cm |
 如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为
如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为
 如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为
如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为