题目内容
如图所示,梯形ABCD中,AB∥DC,AB⊥BC,AB=2,CD=4,以BC上一点O为圆心经过A,D两点,∠AOD=90°,求O到AD的距离.
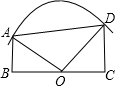

∵∠AOB+∠OAB=90°,∠AOB+∠DOC=90°,
∴∠OAB=∠DOC,
在△ABO与△OCD中,
,
∴△ABO≌△OCD,
∴OB=CD=4.
根据勾股定理得OA=
=2
,AD=
=
=2
.
过O作OF⊥AD,垂足为F.
△AOD是等腰直角三角形,所以OF=
AD=
,即O到AD距离为
.

∴∠OAB=∠DOC,
在△ABO与△OCD中,
|
∴△ABO≌△OCD,
∴OB=CD=4.
根据勾股定理得OA=
| AB2+BO2 |
| 5 |
| AO2+OD2 |
| 62+22 |
| 10 |
过O作OF⊥AD,垂足为F.
△AOD是等腰直角三角形,所以OF=
| 1 |
| 2 |
| 10 |
| 10 |


练习册系列答案
相关题目