题目内容
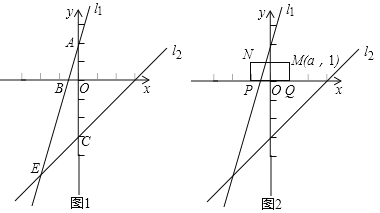
【题目】如图1,在直角坐标系中,一次函数的图象![]() 与
与![]() 轴交于点
轴交于点![]() ,与一次函数
,与一次函数![]() 的图象
的图象![]() 交于点
交于点![]() .
.
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与y轴交于点
与y轴交于点![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(3)如图2,已知矩形![]() ,
,![]() ,
,![]() ,
,![]() ,矩形
,矩形![]() 的边
的边![]() 在
在![]() 轴上平移,若矩形
轴上平移,若矩形![]() 与直线
与直线![]() 或
或![]() 有交点,直接写出
有交点,直接写出![]() 的取值范围,
的取值范围,
【答案】(1)![]() ;(2)
;(2)![]()
![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)由点![]() 在一次函数
在一次函数![]() 图象上可求出E点坐标,然后将AE两点坐标代入解析式即可求出l1的表达式;
图象上可求出E点坐标,然后将AE两点坐标代入解析式即可求出l1的表达式;
(2)由于![]() ,求出BC坐标即可解答
,求出BC坐标即可解答
(3)分别求出矩形MNPQ与直线l1或l2有交点边界时的极限值可解答
(1)∵点![]() 在一次函数
在一次函数![]() 图象上,
图象上,
∴![]() ,
,
∴![]() ;
;
设直线![]() 的表达式为
的表达式为![]() ,
,
∵直线![]() 过点
过点![]() 和
和![]() ,
,
∴![]() ,
,
解得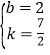 .
.
∴直线![]() 的表达式为
的表达式为![]() .
.
(2)由(1)可知:![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ,
,
∴![]()
![]() .
.
(3)![]() 或
或![]() .
.
当Q在直线![]() 上时,a=
上时,a=![]() ,此时矩形MNPQ与直线
,此时矩形MNPQ与直线![]() 有交点a取最小值,
有交点a取最小值,
当N在直线![]() 上时,N点坐标=
上时,N点坐标=![]() ,a=
,a=![]() ,此时矩形MNPQ与直线
,此时矩形MNPQ与直线![]() 有交点a取最大值,
有交点a取最大值,
当Q在直线![]() 上时,a=2,此时矩形MNPQ与直线
上时,a=2,此时矩形MNPQ与直线![]() 有交点a取最小值,
有交点a取最小值,
当N在直线![]() 上时,N点坐标=4,a=6,此时矩形MNPQ与直线
上时,N点坐标=4,a=6,此时矩形MNPQ与直线![]() 有交点a取最大值,
有交点a取最大值,
故当![]() 时,矩形MNPQ与直线
时,矩形MNPQ与直线![]() 有交点,当2≤a≤6时,矩形MNPQ与直线
有交点,当2≤a≤6时,矩形MNPQ与直线![]() 有交点,
有交点,

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目