题目内容
已知正方形ABCD的边长为2,以BC边为直径作半圆O,P为DC上一动点(可与D重合但不与C重合),连接BP交半圆O于点E,过点O作直线l∥CE交AB(或AD)于点Q.(1)如图1,求证:△OBQ∽△PEC;
(2)设DP=t(0≤t<2),直线l截正方形所得左侧部分图形的面积为S,试求S关于t的函数关系式;
(3)当点Q落在AD(不含端点)上时,问以O、P、Q为顶点的三角形能否是等腰三角形?若能,请指出此时点P的位置;若不能,请说明理由.
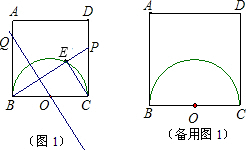
分析:(1)首先根据直径所对的圆周角是直角得到∠BEC=90°,而正方形的内角也为直角,从而得到∠BEC=∠QBC,又根据两直线平行得同位角的相等以及同角的余角相等得到∠BOQ=∠BPC,根据两组对应角相等的两三角形相似,进而得证;
(2)根据时间t的范围分两种情况考虑:当0≤t≤1时,Q在AB上,直线l截正方形所得左侧部分图形为直角三角形,由两对对应角相等的两三角形相似得到△OBQ∽△PBC,得到比例式,求出QB的长,以及OB的长,求出三角形的面积即为所求的S;当1<t<2时,Q在AD上,此时S表示梯形ABOQ面积,过点Q作QM⊥BC,交BC于点M,利用“ASA”证明△QOM≌△BPC,得到OM=CP,表示出CP得到OM的长,再表示出AQ的长,根据梯形的面积公式即可求出S;
(3)利用反证法,方法是根据图形表示出三角形OPQ的三边,分别假设其中的两者相等,推出矛盾,假设错误,故以O、P、Q为顶点的三角形不可能是等腰三角形.
(2)根据时间t的范围分两种情况考虑:当0≤t≤1时,Q在AB上,直线l截正方形所得左侧部分图形为直角三角形,由两对对应角相等的两三角形相似得到△OBQ∽△PBC,得到比例式,求出QB的长,以及OB的长,求出三角形的面积即为所求的S;当1<t<2时,Q在AD上,此时S表示梯形ABOQ面积,过点Q作QM⊥BC,交BC于点M,利用“ASA”证明△QOM≌△BPC,得到OM=CP,表示出CP得到OM的长,再表示出AQ的长,根据梯形的面积公式即可求出S;
(3)利用反证法,方法是根据图形表示出三角形OPQ的三边,分别假设其中的两者相等,推出矛盾,假设错误,故以O、P、Q为顶点的三角形不可能是等腰三角形.
解答:解:(1)∵直径所对的圆周角为90°,
∴∠BEC=90°=∠QBC,
∵直线l∥CE交AB(或AD)于点Q.
∴∠BOQ=∠BCE,
又∠BCE+∠PCE=90°,∠PCE+∠BPC=90°,
∴∠BOQ=∠BPC,
∴△OBQ∽△PEC;
(2)当0≤t≤1时,Q在AB上,
∵∠OBQ=∠PCB=90°,
又∵∠PBC+∠QOB=90°,∠QOB+∠BQO=90°,
∴∠PBC=∠BQO,
∴△OBQ∽△PBC,
∴QB:BC=BO:PC,即QB:2=1:(2-t),
解得:QB=
,又OB=
BC=1,
则S=
OB•QB=
;
当1<t<2时,Q在AD上,此时S表示梯形ABOQ面积,
根据题意画出图形,如图所示:
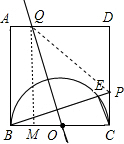
过点Q作QM⊥BC,交BC于点M,
∵ABCD为正方形,
∴∠QMO=∠BCP=90°,AB=BC=QM,
又∠QOM+∠OQM=90°,∠QOM+∠PBC=90°,
∴∠OQM=∠PBC,
∴△QOM≌△BPC,
又DP=t,DC=2,得到:CP=2-t,
∴OM=PC=2-t,
∴AQ=1-(2-t)=t-1,
则S=
=t;
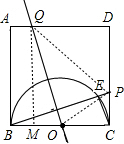
(3)当Q在AD上(不含端点)上时,
连接PQ,由QM=2,OM=2-t,
根据勾股定理得:OQ2=4+(2-t)2=t2-4t+8,
又QD=2-(t-1)=3-t,DP=t,
根据勾股定理得:QP2=(3-t)2+t2=2t2-6t+9,
连接OP,由PC=2-t,OC=1,
根据勾股定理得:OP2=12+(2-t)2=t2-4t+5,
显然OP≠OQ;
假设OP=PQ,即2t2-6t+9=t2-4t+5,
解得t=2,
P与C重合,不合题意,假设错误,故OP≠PQ,
若OQ=PQ,t2-4t+8=2t2-6t+9,
整理得:t2-2t+1=0,即(t-1)2=0,
解得:t=1,
不合题意,假设错误,故OQ≠PQ;
∴当Q落在AD(不含端点)上时,以O、P、Q为顶点的三角形不可能是等腰三角形.
∴∠BEC=90°=∠QBC,
∵直线l∥CE交AB(或AD)于点Q.
∴∠BOQ=∠BCE,
又∠BCE+∠PCE=90°,∠PCE+∠BPC=90°,
∴∠BOQ=∠BPC,
∴△OBQ∽△PEC;
(2)当0≤t≤1时,Q在AB上,
∵∠OBQ=∠PCB=90°,
又∵∠PBC+∠QOB=90°,∠QOB+∠BQO=90°,
∴∠PBC=∠BQO,
∴△OBQ∽△PBC,
∴QB:BC=BO:PC,即QB:2=1:(2-t),
解得:QB=
| 2 |
| 2-t |
| 1 |
| 2 |
则S=
| 1 |
| 2 |
| 1 |
| 2-t |
当1<t<2时,Q在AD上,此时S表示梯形ABOQ面积,
根据题意画出图形,如图所示:

过点Q作QM⊥BC,交BC于点M,
∵ABCD为正方形,
∴∠QMO=∠BCP=90°,AB=BC=QM,
又∠QOM+∠OQM=90°,∠QOM+∠PBC=90°,
∴∠OQM=∠PBC,
∴△QOM≌△BPC,
又DP=t,DC=2,得到:CP=2-t,
∴OM=PC=2-t,
∴AQ=1-(2-t)=t-1,
则S=
| 2(t-1+1) |
| 2 |

(3)当Q在AD上(不含端点)上时,
连接PQ,由QM=2,OM=2-t,
根据勾股定理得:OQ2=4+(2-t)2=t2-4t+8,
又QD=2-(t-1)=3-t,DP=t,
根据勾股定理得:QP2=(3-t)2+t2=2t2-6t+9,
连接OP,由PC=2-t,OC=1,
根据勾股定理得:OP2=12+(2-t)2=t2-4t+5,
显然OP≠OQ;
假设OP=PQ,即2t2-6t+9=t2-4t+5,
解得t=2,
P与C重合,不合题意,假设错误,故OP≠PQ,
若OQ=PQ,t2-4t+8=2t2-6t+9,
整理得:t2-2t+1=0,即(t-1)2=0,
解得:t=1,
不合题意,假设错误,故OQ≠PQ;
∴当Q落在AD(不含端点)上时,以O、P、Q为顶点的三角形不可能是等腰三角形.
点评:此题综合考查了相似三角形的性质与判定,正方形的性质以及勾股定理.学生作(2)时注意根据Q的位置分两种情况考虑,(3)采用的方法是反证法,注意反证法的步骤:先否定结论,根据推理得到与已知,定理及公理矛盾,得到假设错误,所以原命题正确.

练习册系列答案
相关题目
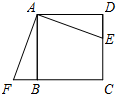 如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为
如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为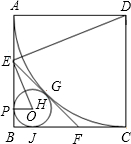 合),过点E作弧AC的切线,交BC于点F,G为切点,⊙O是△EBF的内切圆,分别切EB、BF、FE于点P、J、H
合),过点E作弧AC的切线,交BC于点F,G为切点,⊙O是△EBF的内切圆,分别切EB、BF、FE于点P、J、H (2011•同安区质检)如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE.
(2011•同安区质检)如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE.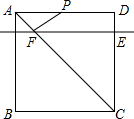 (2012•香洲区一模)如图,已知正方形ABCD的边长为28,动点P从A开始在线段AD上以每秒3个单位长度的速度向点D运动(点P到达点D时终止运动),动直线EF从AD开始以每秒1个单位长度的速度向下平行移动(即EF∥AD),并且分别与DC、AC交于E、F两点,连接FP,设动点P与动直线EF同时出发,运动时间为t 秒.
(2012•香洲区一模)如图,已知正方形ABCD的边长为28,动点P从A开始在线段AD上以每秒3个单位长度的速度向点D运动(点P到达点D时终止运动),动直线EF从AD开始以每秒1个单位长度的速度向下平行移动(即EF∥AD),并且分别与DC、AC交于E、F两点,连接FP,设动点P与动直线EF同时出发,运动时间为t 秒. 如图,已知正方形ABCD的边长为8cm,点E、F分别在边BC、CD上,∠EAF=45°.当EF=8cm时,△AEF的面积是
如图,已知正方形ABCD的边长为8cm,点E、F分别在边BC、CD上,∠EAF=45°.当EF=8cm时,△AEF的面积是