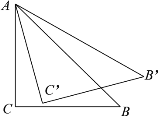
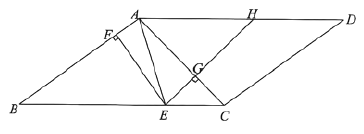
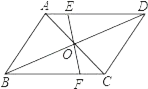
题目内容
【题目】如图①,在平面直角坐标系中,直线![]() :
:![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() ,且与直线
,且与直线![]() :
:![]() 交于点
交于点![]() ,以线段
,以线段![]() 为边在直线
为边在直线![]() 的下方作正方形
的下方作正方形![]() ,此时点
,此时点![]() 恰好落在
恰好落在![]() 轴上.
轴上.
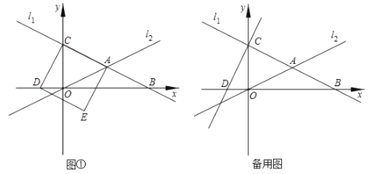
(1)求出![]() 三点的坐标.
三点的坐标.
(2)求直线![]() 的函数表达式.
的函数表达式.
(3)在(2)的条件下,点![]() 是射线
是射线![]() 上的一个动点,在平面内是否存在点
上的一个动点,在平面内是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,直接写出点
为顶点的四边形是菱形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]()
![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() ,
,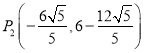 ,
,![]() .
.
【解析】
(1)利用一次函数图象上点的坐标特征可求出点B,C的坐标,联立直线l1,l2的解析式成方程组,通过解方程组可求出点A的坐标;
(2)过点A作AF⊥y轴,垂足为点F,则△ACF≌△CDO,利用全等三角形的性质可求出点D的坐标,根据点C,D的坐标,利用待定系数法即可求出直线CD的解析式;
(3)分OC为对角线及OC为边两种情况考虑:①若OC为对角线,由菱形的性质可求出点P的纵坐标,再利用一次函数图象上点的坐标特征可求出点P1的坐标;②若OC为边,设点P的坐标为(m,2m+6),分CP=CO和OP=OC两种情况,利用两点间的距离公式可得出关于m的方程,解之取其负值,再将其代入点P的坐标中即可得出点P2,P3的坐标.
(1)∵直线![]() :
:![]() ,
,
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
∴![]() ,
,![]() ,
,
解方程组: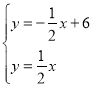 得:
得:![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
(2)如图1,作![]() ,则
,则![]() ,
,
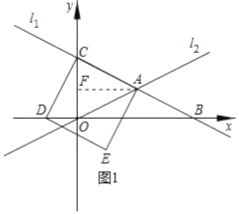
∵四边形![]() 为正方形,
为正方形,
∴![]() ,
,![]()
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]()
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
设直线![]() 的解析式为
的解析式为![]() ,
,
将![]() 、
、![]() 代入得:
代入得:![]() ,
,
解得:![]() ,
,
∴直线![]() 的解析式为
的解析式为![]()
(3)存在
①以![]() 为对角线时,如图2所示,
为对角线时,如图2所示,
则PQ垂直平分CO,
则点P的纵坐标为:![]() ,
,
当y=3时,![]() ,解得:x=
,解得:x=![]()
∴点![]() ;
;
②以![]() 为边时,如图2,设点P(m,2m+6),
为边时,如图2,设点P(m,2m+6),
当CP=CO时,![]() ,
,
解得:![]() (舍去)
(舍去)
∴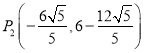 ,
,
当OP=OC时,![]() ,
,
解得:![]() (舍去)
(舍去)
∴![]()
综上所述,在平面内是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形,
为顶点的四边形是菱形,![]() ,
,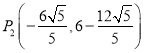 ,
,![]() .
.


【题目】在数学课上,老师出了这样一道题:甲、乙两地相距1400km,乘高铁列车从甲地到乙地比乘特快列车少用9h,已知高铁列车的平均行驶速度是特快列车的2.8倍.求高铁列车从甲地到乙地的时间.
老师要求同学先用列表方式分析再解答.下面是两个小组分析时所列的表格:
小组甲:设特快列车的平均速度为![]() km/h.
km/h.
时间/h | 平均速度/(km/h) | 路程/km | |
高铁列车 | 1400 | ||
特快列车 |
| 1400 |
小组乙:高铁列车从甲地到乙地的时间为![]() h.
h.
时间/h | 平均速度/(km/h) | 路程/km | |
高铁列车 |
| 1400 | |
特快列车 | 1400 |
(1)根据题意,填写表格中空缺的量;
(2)结合表格,选择一种方法进行解答.