题目内容
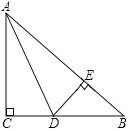
【题目】已知:如图,∠B=90°,AB∥DF,AB=3cm,BD=8cm,点C是线段BD上一动点,点E是直线DF上一动点,且始终保持AC⊥CE.
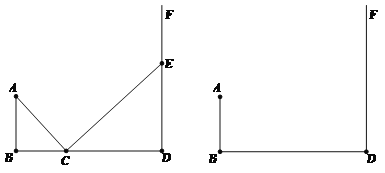
(1)试说明:∠ACB =∠CED
(2)若AC=CE ,试求DE的长
(3)在线段BD的延长线上,是否存在点C,使得AC=CE,若存在,请求出DE的长及△AEC的面积;若不存在,请说明理由。
【答案】(1)说明见解析; (2)5cm;(3)65cm2.
【解析】
试题(1)根据平行线的性质和三角形的内角和定理求出即可;
(2)根据全等得出对应边相等,即可得出答案;
(3)求出两三角形全等,得出对应边相等,再根据勾股定理和三角形面积公式求出即可.
试题解析:(1)∵∠B=90°,AB∥DF,
∴∠D=∠B=90°,
∵AC⊥CE,
∴∠ACE=90°,
∴∠ECD+∠CED=90°,∠ACB+∠ECD=90°,
∴∠ACB=∠CED;
(2)∵在△ABC和△CDE中

∴△ABC≌△CDE(AAS),
∴AB=CD=3cm,
∴DE=BC=8cm-3cm=5cm;
(3)∵∠B=90°AB∥DF,
∴∠CDE=∠B=90°,
∵AC⊥CE,
∴∠ACE=90°,
∴∠ECD+∠ACB=90°,∠ACB+∠BAC=90°,
∴∠ECD=∠BAC;
当CD=AB=3cm时,AC=CE,
∵在△ABC和△CDE中

∴△ABC≌△CDE(ASA),
∴AC=CE,DE=BD=8cm,
∵AB=3cm,BC=BD+CD=8cm+3cm=11cm,
∴在Rt△ABC中,由勾股定理得;AC=![]()
∵∠ACE=90°,
∴△AEC的面积是![]() ×AC×CE=
×AC×CE=![]() ×
×![]() ×
×![]() =65cm2.
=65cm2.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目