题目内容
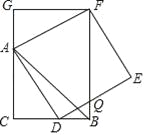
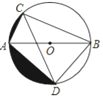
【题目】如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=5,BC=3.
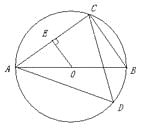
(1) 求sin∠BAC的值;
(2) 如果OE⊥AC, 垂足为E,求OE的长;
(3) 求tan∠ADC的值.(结果保留根号)
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)根据圆周角定理可得到∠ACB是直角,再根据三角函数求解即可;
(2)首先根据垂径定理得出E是AC中点.再根据中位线定理求解即可;
(3)根据同弧或等弧所对的圆周角相等可得∠ADC=∠ABC,在Rt![]() ACB中求出tan∠ABC即可.
ACB中求出tan∠ABC即可.
解:(1)∵AB是⊙O直径
∴∠ACB=90°
∵AB=5,BC=3
∴sin∠BAC==![]() ;
;
(2)∵OE⊥AC,O是⊙O的圆心
∴E是AC中点.
又∵O是AB的中点.
∴OE=![]() BC=
BC=![]() ;
;
(3)在Rt![]() ACB中,∠ACB=90°
ACB中,∠ACB=90°
∵AB=5,BC=3
∴AC=![]() =4
=4
∵∠ADC=∠ABC
∴tan∠ADC=tan∠ABC=![]() .
.

练习册系列答案
相关题目
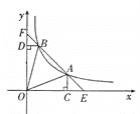
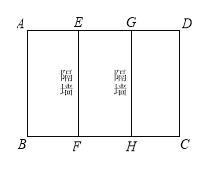
【题目】如图,在左边托盘A(固定)中放置一个生物,在右边托盘B(可左右移动)中放置一定重量的砝码,可使得仪器左右平衡,改变托盘B与支撑点M的跳高,记录相应的托盘B中的砝码质量,得到下表:
托盘B与点M的距离x(cm) | 10 | 15 | 20 | 25 | 30 |
托盘B中的砝码质量y(g) | 30 | 20 | 15 | 12 | 10 |
(1)把上表中(x,y)的各级对应值作为点的坐标,在如图所示的平面直角坐标系中描出其余的点,并用一条光滑的曲线连接起来,观察所画的图象,猜想y与x的函数关系,求出该函数关系式.
(2)当托盘B向左移动(不能超过点M)时,应往托盘B中添加砝码还是减少砝码?为什么?