Question

【题目】如图，AB是⊙O直径，OC⊥AB，弦CD与OB交于点F，过点D、A分别作⊙O的切线交于点G，切线GD与AB延长线交于点E．

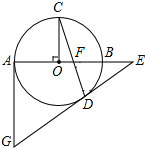
（1）求证：∠C+∠EDF=90°

（2）已知：AG=6，⊙O的半径为3，求OF的值．

Answer 1

【答案】（1）见解析；（2）1

【解析】

试题分析：（1）连接OD，根据切线的性质得OD⊥DE，则∠EDF+∠ODC=90°，而∠C=∠ODC，则∠EDF+∠C=90°．

（2）先求得EF=ED，设DE=x，则EF=x，根据切线的性质由AG为⊙O的切线得∠ODE=90°，再证明Rt△EOD∽Rt△EGA，利用相似比求得AE=2x，OE=3+x，然后根据AE﹣OE=OA=3，求得x的值，进而求得OF=1．

（1）证明：连接OD，

∵DE为⊙O的切线，

∴OD⊥DE，

∴∠ODE=90°，即∠EDF+∠ODC=90°，

∵OC=OD，

∴∠C=∠ODC，

∴∠C+∠EDF=90°．

（2）解：∵∠C+∠EDF=90°，∠C+∠CFO=90°，∠CFO=∠EFD，

∴∠EFD=∠EDF，

∴EF=ED，

设DE=x，则EF=x，

∵∠ODE=∠GAE，∠OED=∠GEA，

∴Rt△EOD∽Rt△EGA，

∴==，即==，

∴AE=2x，OE=3+x，

∵AE﹣OE=OA=3，

∴2x﹣（3+x）=3，解得x=4，

∴AE=2x=8，

∴OF=AE﹣EF﹣OA=8﹣3﹣4=1．