题目内容
【题目】已知,AB是半圆O的直径,弦CD∥AB,动点M、N分别在线段OC、CD上,AM的延长线与射线ON相交于点E,与弦CD相交于点F.
(1)如图1,若DN=OM,求证:AM=ON; 
(2)如图2,点P是弦CD上一点,若AP=OP,∠APO=90°,求∠COP的度数; 
(3)在(1)的条件下,若AB=20,cos∠AOC= ![]() ,当点E在ON的延长线上,且NE=NF时,求线段EF的长.
,当点E在ON的延长线上,且NE=NF时,求线段EF的长. 
【答案】
(1)解:如图1,
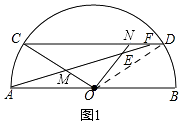
连接OD,
∴OA=OD,
∵CD∥AB,
∴∠BOD=∠NDO, ![]() ,
,
∴∠AOC=∠BCD,
∴∠AOC=∠CDO,
在△AMO和△OND中, 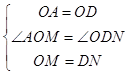 ,
,
∴△AMO≌△OND,
∴AM=ON,
(2)解:如图2,
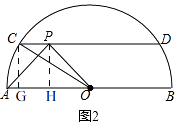
过点C作CG⊥AB,PH⊥AB,
∴CG=PH,
∵AP=OP,∠APO=90°,
∴∠AOP=45°,PH= ![]() OA,
OA,
∴CG= ![]() OA=
OA= ![]() OC,
OC,
∴∠AOC=30°,
∴∠COP=∠AOP﹣∠AOC=15°
(3)解:如图3,
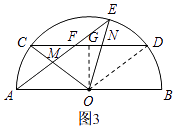
作OG⊥CD于G,连接OD,
∵AB=20,
∴OC=10
CG=OCcos∠C=OCcos∠AOC=10× ![]() =8
=8
∴CD=2CG=16
∵NE=NF,
∴∠E=∠EFN
∵CD∥AB,
∴∠EFN=∠A
∴∠E=∠A,
∴OE=OA
∵CD∥AB,
∴∠BOD=∠D=∠C=∠AOC
∴∠AOE=∠COD
∴△AOE≌△COD,
∴AE=CD=16
∵△AOM≌△ODN,
∴∠NOD=∠A=∠E
∴AE∥OD,
∴四边形AODF是平行四边形
∴AF=OD=10
∴EF=AE﹣AF=16﹣10=6
【解析】(1)先判断出∠BOD=∠NDO, ![]() 进而得出∠AOC=∠CDO,即可得出△AMO≌△OND,结论得证;(2)构造出直角三角形,先判断出PH=
进而得出∠AOC=∠CDO,即可得出△AMO≌△OND,结论得证;(2)构造出直角三角形,先判断出PH= ![]() OA,即可得出CG=
OA,即可得出CG= ![]() OC,进而求出∠AOC=30°,最后用角的差,即可得出结论.(3)先求出CD=2CG=16,再判断出△AOE≌△COD,进而判断出四边形AODF是平行四边形,最后用线段的差即可得出结论;
OC,进而求出∠AOC=30°,最后用角的差,即可得出结论.(3)先求出CD=2CG=16,再判断出△AOE≌△COD,进而判断出四边形AODF是平行四边形,最后用线段的差即可得出结论;