题目内容
如图,AB∥CD.(1)如果∠BAE=∠DCE=45°,求∠E的度数.请将下面解题过程补充完整.
∵AB∥CD(已知)
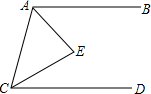
∴∠BAC+∠DCA=180°(
∴∠EAC+∠BAE+∠ACE+∠DCE=180°∵∠BAE=∠DCE=45°(已知)
∴∠EAC+
∴∠EAC+∠ACE=
∵∠EAC+∠ACE+∠E=180°(
∴∠E=180°-(
(2)如果AE、CE分别是∠BAC、∠DCA的平分线,(1)中的结论还成立吗?试说明理由.
(3)如果AE、CE分别是∠BAC、∠DCA内部的任意射线.求证:∠AEC=∠BAE+∠DCE.
分析:(1)我们可以倒推,根据三角形的内角和等于180度?∠E=180°-(∠EAC+∠ACE),根据两直线平行,同旁内角互补的性质?∠EAC+∠ACE=180°-(∠BAE+∠DCE),由此可知∠E=90°;
(2)如果AE、CE分别是∠BAC、∠DCA的平分线,根据两直线平行,同旁内角互补的性质?∠EAC+∠ACE=90°,根据三角形的内角和等于180度,?∠E=180°-(∠EAC+∠ACE)=90°;
(3)根据三角形的内角和等于180度?∠E=180°-(∠EAC+∠ACE),根据两直线平行,同旁内角互补的性质?∠BAE+∠DCE
=180°-(∠EAC+∠AEC)?∠E=∠BAE+∠DCE
(2)如果AE、CE分别是∠BAC、∠DCA的平分线,根据两直线平行,同旁内角互补的性质?∠EAC+∠ACE=90°,根据三角形的内角和等于180度,?∠E=180°-(∠EAC+∠ACE)=90°;
(3)根据三角形的内角和等于180度?∠E=180°-(∠EAC+∠ACE),根据两直线平行,同旁内角互补的性质?∠BAE+∠DCE
=180°-(∠EAC+∠AEC)?∠E=∠BAE+∠DCE
解答:解:(1)两直线平行,同旁内角互补;45°;45°;等量代换;90°;
三角形的内角和等于180°;∠EAC+∠ACE;90°.
(2)∵AB∥CD(已知)
∴∠BAC+∠DCA=180°( 两直线平行,同旁内角互补)
∴AE、CE分别是∠BAC、∠DCA的平分线(已知)
∴∠EAC+∠ACE=
∠BAC+
∠DCA=90°(角平分线的性质)
∵∠EAC+∠ACE+∠E=180°( 三角形的内角和等于180°)
∴∠E=180°-(∠EAC+∠ACE)=90°
(3)∵AB∥CD(已知)
∴∠BAE+∠DCE=180°-(∠EAC+∠AEC)( 两直线平行,同旁内角互补)
∵∠EAC+∠ACE+∠E=180°( 三角形的内角和等于180°)
∴∠E=180°-(∠EAC+∠ACE)
∴∠E=∠BAE+∠DCE(等量代换)
三角形的内角和等于180°;∠EAC+∠ACE;90°.
(2)∵AB∥CD(已知)
∴∠BAC+∠DCA=180°( 两直线平行,同旁内角互补)
∴AE、CE分别是∠BAC、∠DCA的平分线(已知)
∴∠EAC+∠ACE=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠EAC+∠ACE+∠E=180°( 三角形的内角和等于180°)
∴∠E=180°-(∠EAC+∠ACE)=90°
(3)∵AB∥CD(已知)
∴∠BAE+∠DCE=180°-(∠EAC+∠AEC)( 两直线平行,同旁内角互补)
∵∠EAC+∠ACE+∠E=180°( 三角形的内角和等于180°)
∴∠E=180°-(∠EAC+∠ACE)
∴∠E=∠BAE+∠DCE(等量代换)
点评:本题重点考查两直线平行,同旁内角互补,等量代换,三角形内角和定理等性质的综合应用,在求证过程中注意于等量之间的代换、准确地识别图形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
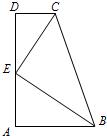 23、如图,AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD中点.求证:CE⊥BE.
23、如图,AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD中点.求证:CE⊥BE.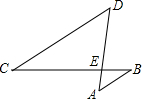 如图,AB∥CD,AD与BC相交于点E,如果AB=2,CD=6,AE=1,那么DE=
如图,AB∥CD,AD与BC相交于点E,如果AB=2,CD=6,AE=1,那么DE=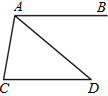 4、如图,AB∥CD,∠C=80°,∠CAD=60°,则∠BAD的度数等于( )
4、如图,AB∥CD,∠C=80°,∠CAD=60°,则∠BAD的度数等于( ) 34、如图,AB∥CD,P是BC上的一个动点,设∠CDP=∠1,∠CPD=∠2,请你猜想出∠1、∠2与∠B之间的关系,并说明理由.
34、如图,AB∥CD,P是BC上的一个动点,设∠CDP=∠1,∠CPD=∠2,请你猜想出∠1、∠2与∠B之间的关系,并说明理由. 如图,AB∥CD,∠1=58°,则∠2的度数是( )
如图,AB∥CD,∠1=58°,则∠2的度数是( )