题目内容
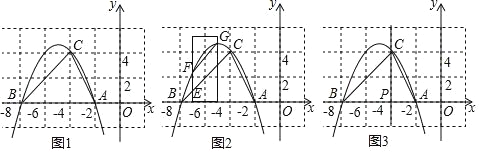
【题目】如图1,抛物线y=﹣![]() x2+bx+c经过点A(﹣2,0),B(﹣8,0),C(﹣4,4).
x2+bx+c经过点A(﹣2,0),B(﹣8,0),C(﹣4,4).
(1)求这个抛物线的表达式;
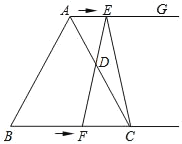
(2)如图2,一把宽为2的直尺的右边缘靠在直线x=﹣4上,当直尺向左平移过程中刻度线0始终在x轴上,直尺的右边边缘与抛物线和直线BC分别交于G、D点,直尺的左边边缘与抛物线和直线BC分别交于F、E点,当图中四边形DEFG是平行四边形时,此时直尺左边边缘与直线BC的交点E的刻度是多少?
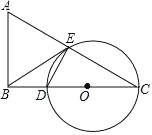
(3)如图3,在直线x=﹣4上找一点K,使得∠ACP+∠AKC=∠ABC(直线x=﹣4与x轴交于P点),请直接写出K点的坐标.
【答案】(1)y=![]() x2-5x-8,
x2-5x-8,
(2)E(-7,1)
(3)K(-4,6)或(-4,-6).
【解析】
(1)将A(-2,0),B(-8,0)代入函数解析式即可求解,
(2)根据图像性质求出直线BC的解析式为y=x+8,设D(a,a+8),再表示出G(a,![]() a2-5a-8),E(a-2,a+6), F(a-2,
a2-5a-8),E(a-2,a+6), F(a-2,![]() a2-3a),根据DG=EF即可解题,
a2-3a),根据DG=EF即可解题,
(3)根据网格点特征,即可求出K的坐标.
解:(1)将点A(-2,0),B(-8,0)代入y=![]() x2+bx+c中得:b=-5,c=-8,
x2+bx+c中得:b=-5,c=-8,
∴抛物线的解析式是y=![]() x2-5x-8,
x2-5x-8,
(2)如下图,
∵A(-2,0),B(-8,0),C(-4,4),
∴直线BC的解析式为y=x+8,
根据题意可知∠ABC=45°,
∴设D(a,a+8),则G(a,![]() a2-5a-8),
a2-5a-8),
E(a-2,a+6),则F(a-2,![]() a2-3a),
a2-3a),
∵四边形ABCD是平行四边形,
∴DG=EF即![]() a2-5a-8-(a+8)=
a2-5a-8-(a+8)=![]() a2-3a-(a+6),
a2-3a-(a+6),
解得:a=-5,
∴E(-7,1)

(3)由题可知∠ABC=45°,即在直线x=-4上找一点K,使得∠ACP+∠AKC=45°,
根据网格的特征即可找到点K(-4,6)或(-4,-6).

 阅读快车系列答案
阅读快车系列答案