Question

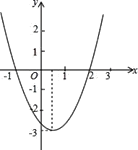
【题目】抛物线y=x+2x-3与x轴相交于A、B两点，其顶点为M，将此抛物线在x轴下方的部分沿x轴翻折，其余部分保持不变，得到一个新的图象，如图．在这个新图象上有一点P，能使得S△ABP=6，则点P的坐标为___________.

Answer 1

【答案】（- 1+，3）或（-1-，3）或（-2,3）或（0，3）

【解析】

先求出A，B两点的坐标，从而求出AB的长，再根据面积计算公式列方程 求解即可.

把y=0代入y=x+ 2x -3得x+2x-3=0，解得x=-3,x=1∴A（-3,0），B（1,0），∴AB=4.∵y=x+2x-3=(x+1)-4,∴M（-1，-4）．将此抛物线在x轴下方的部分沿x轴翻折，此时向上翻折部分的抛物线的顶点坐标为（-1，4）．由于抛物线翻折，开口方向改变，形状不变，则向上翻折部分抛物线的式为y=-（x+1）+4= -x-2x+3（-3≤x≤1）．设点P的横坐标为a，当点P在原抛物线y=x+2x-3上时（x轴上方的部分），可得×4×(a+2a-3)=6，解得a=-1+，a=-1-,∴P（-1+，3）．P（-1-，3），当点P在新抛物线y=-x-2x+3上时（x轴上方的部分），可得×4×(-a-2a+3)=6，解得a=-2，a=0，∴P（-2,3），P(0,3).综上，点P的坐标为（-1+，3）或（-1-，3）或（-2，3）或(0，3).