题目内容
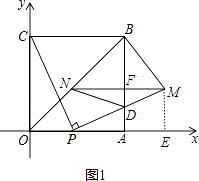
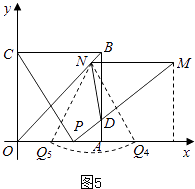
【题目】如图，四边形OABC是边长为4的正方形，点P为OA边上任意一点（与点O、A不重合），连接CP，过点P作PM⊥CP交AB于点D，且PM=CP，过点M作MN∥AO，交BO于点N，连结ND、BM，设OP=t．
（1）求点M的坐标（用含t的代数式表示）；
（2）试判断线段MN的长度是否随点P的位置的变化而改变？并说明理由．
（3）当t为何值时，四边形BNDM的面积最小；
（4）在x轴正半轴上存在点Q，使得△QMN是等腰三角形，请直接写出不少于4个符合条件的点Q的坐标（用含t的式子表示）．
【答案】
（1）
解：如图1所示，作ME⊥OA于点E，
∴∠MEP=∠POC=90°，
∵PM⊥CP，
∴∠CPM=90°，
∴∠OPC+∠MPE=90°，
又∵∠OPC+∠PCO=90°，
∴∠MPE=∠PCO，
∵PM=CP，
∴△MPE≌△PCO（AAS），
∴PE=CO=4，ME=PO=t，
∴OE=4+t，
∴点M的坐标为（4+t，t）（0＜t＜4）
（2）
解：线段MN长度不变，
理由：∵OA=AB=4，
∴点B（4，4），
∴直线OB的解析式为：y=x，
∵点N在直线OB上，MN∥OA，M（4+t，t），
∴点N（t，t），
∵MN∥OA，M（4+t，t），
∴MN=|（4+t）﹣t|=4，
即MN的长度不变
（3）
解：由（1）知，∠MPE=∠PCO，
又∵∠DAP=∠POC=90°，
∴△DAP∽△POC，
∴ 
，
∵OP=t，OC=4，
∴AP=4﹣t，
∴ 
，得AD= 
，
∴BD=4﹣ = 
，
∵MN∥OA，AB⊥OA，
∴MN⊥BD，
∵ 
= 
= 
，
∴当t=2时，四边形BNDM的面积最小，最小值6
（4）
解：在x轴正半轴上存在点Q，使得△QMN是等腰三角形，此时点Q的坐标为：Q1（t+2，0），Q2（4+t﹣ 
，0），Q3（4+t+ ，0）Q4（t+ ，0）其中（0＜t＜4），Q5（t﹣ ，0）
理由：当（2）可知，OP=t（0＜t＜4），MN=PE=4，MN∥x轴，所以共分为以下几种请：
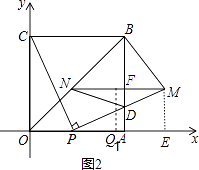
第一种情况：当MN为底边时，作MN的垂直平分线，与x轴的交点为Q1，如图2所示
=2，
∴OQ1=t+2，
∴Q1（t+2，0）
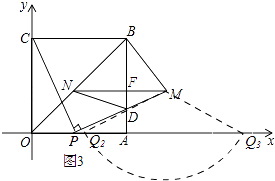
第二种情况：如图3所示，当MN为腰时，以M为圆心，MN的长为半径画弧交x轴于点Q2、Q3，连接MQ2、MQ3，则MQ2=MQ3=4，
∴Q2E= 
，
∴OQ2=OE﹣Q2E=4+t﹣ ，
∴Q2（4+t﹣ ，0），
∵Q3E=Q2E，
∵OQ3=OE+Q3E=4+t+ ，
∴Q3（4+t+ ，0）；
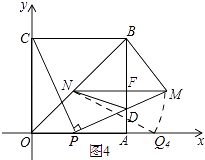
第三种情况，当MN为腰时，以N为圆心，MN长为半径画圆弧交x轴正半轴于点Q4，
当0＜t＜2 
时，如图4所示，
则PQ4= 
= ，
∴OQ4=OP+PQ4=t+ ，
即Q4（ 
，0）．
当t=2 时，
则ON=4，此时Q点与O点重合，舍去；
当2 ＜t＜4时，如图5，以N为圆心，MN为半径画弧，与x轴的交点为Q4，Q5．
Q4的坐标为：Q4（ 
，0）．
OQ5=t﹣ ，
∴Q5（t﹣ ，0）
所以，综上所述，当0＜t＜4时，在x轴的正半轴上存在5个点Q，分别为Q1（t+2，0），Q2（4+t﹣ ，0），Q3（4+t+ ，0）Q4（t+ ，0），Q5（t﹣ ，0）使△QMN是等腰三角形
【解析】（1）作ME⊥OA于点E，要求点M的坐标只要证明△OPC≌△EM即可，根据题目中的条件可证明两个三角形全等，从而可以得到点M的坐标；（2）首先判断是否变化，然后针对判断结合题目中的条件说明理由即可解答本题；（3）要求t为何值时，四边形BNDM的面积最小，只要用含t的代数式表示出四边形的面积，然后化为顶点式即可解答本题；（4）首先写出符合要求的点Q的坐标，然后根据写出的点的坐标写出推导过程即可解答本题．本题考查四边形综合题，解题的关键是明确题意，画出相应的图象，找出所求问题需要的条件，利用数形结合的思想解答问题．
【考点精析】解答此题的关键在于理解全等三角形的性质的相关知识，掌握全等三角形的对应边相等; 全等三角形的对应角相等．
