��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У�ֱ��![]() Ϊһ��������ƽ���ߣ���P����y��ĶԳƵ��ΪP��һ�η���㣬����
Ϊһ��������ƽ���ߣ���P����y��ĶԳƵ��ΪP��һ�η���㣬����![]() ��
��![]() ����ֱ��
����ֱ��![]() �ĶԳƵ��Ϊ��P�Ķ��η���㣬����
�ĶԳƵ��Ϊ��P�Ķ��η���㣬����![]() �����磬��
�����磬��![]() ��һ�η����Ϊ
��һ�η����Ϊ![]() �����η����Ϊ
�����η����Ϊ![]() �����ݶ��壬�ش��������⣺
�����ݶ��壬�ش��������⣺
��1����![]() ��һ�η����Ϊ________�����η����Ϊ__________��
��һ�η����Ϊ________�����η����Ϊ__________��
��2������A�ڵ�һ����ʱ����![]() ��
��![]() ��
��![]() �п����ǵ�A�Ķ��η�������_________��
�п����ǵ�A�Ķ��η�������_________��
��3������A�ڵڶ����ޣ���![]() ��
��![]() �ֱ��ǵ�A��һ�Ρ����η���㣬��
�ֱ��ǵ�A��һ�Ρ����η���㣬��![]() Ϊ�ȱ������Σ�������OA��x��������ǵĶ�����
Ϊ�ȱ������Σ�������OA��x��������ǵĶ�����
���𰸡���1��![]() ��
��![]() �� ��2��N�㣻 ��3������OA��x���������Ϊ
�� ��2��N�㣻 ��3������OA��x���������Ϊ![]() ��
��![]() ��
��
��������
��1�����ݷ���Ķ�����⣻��2�����ݷ��䶨���֪��A�Ķ��η�����ڵ��������3�����ݷ��䶨��õ�![]() ���ڵ�һ���ޣ� ��
���ڵ�һ���ޣ� ��![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�![]() ����OB�Գƣ���
����OB�Գƣ���![]() ��������
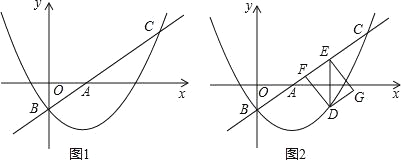
��������![]() λ��ֱ��l���Ϸ�����ͼ1��ʾ����ʱ
λ��ֱ��l���Ϸ�����ͼ1��ʾ����ʱ![]() ������
������![]() λ��ֱ��l�����·�����ͼ2��ʾ����ʱ
λ��ֱ��l�����·�����ͼ2��ʾ����ʱ![]()
�⣺��1��![]() ��
��![]() ��
��
��2��N�㣻
��3���ߵ�A�ڵڶ����ޣ�
���![]() ���ڵ�һ���ޣ�
���ڵ�һ���ޣ�
�ߡ�![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�![]() ����OB�Գƣ�
����OB�Գƣ�
��![]()
�������ۣ�
������![]() λ��ֱ��l���Ϸ�����ͼ1��ʾ��
λ��ֱ��l���Ϸ�����ͼ1��ʾ��
��ʱ![]()
�������OA��x���������Ϊ![]() ��
��
������![]() λ��ֱ��l�����·�����ͼ2��ʾ��
λ��ֱ��l�����·�����ͼ2��ʾ��
��ʱ![]()
�������OA��x���������Ϊ![]() ��
��
��������������OA��x���������Ϊ![]() ��
��![]() ��
��

ͼ1 ͼ2

����Ŀ��ij�н�ʵ�о��������õ���ݵ�۷��������±���ͼ�����߷�ӳ��ÿ������ÿ�µ��![]() ��Ԫ�����õ���
��Ԫ�����õ���![]() ���ȣ���ĺ�����ϵ.
���ȣ���ĺ�����ϵ.
���� | ��һ�� | �ڶ��� | ������ |
ÿ���õ��� |
|
|
|
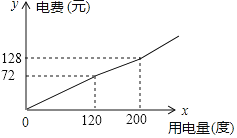
��1��С����ij���õ�![]() �ȣ��轻���___________Ԫ��
�ȣ��轻���___________Ԫ��
��2����ڶ������![]() ��Ԫ�����õ���
��Ԫ�����õ���![]() ���ȣ�֮��ĺ�����ϵʽ��
���ȣ�֮��ĺ�����ϵʽ��
��3��С����ij���õ�![]() �ȣ����ɵ��
�ȣ����ɵ��![]() Ԫ���������������ÿ�ȵ�ѱȵڶ���ÿ�ȵ�Ѷ����Ԫ��
Ԫ���������������ÿ�ȵ�ѱȵڶ���ÿ�ȵ�Ѷ����Ԫ��
����Ŀ�����ڴ���ʽ����ͬ�ı�����ʽ�ܱ��ֳ����IJ�ͬ���ʣ��������ʽ![]() ��������д��
��������д��![]() ����ʽ�����ܿ���������ĸxȡ��ֵ��������ʾ������������д��
����ʽ�����ܿ���������ĸxȡ��ֵ��������ʾ������������д��![]() ����ʽ�����������ʽB=
����ʽ�����������ʽB=![]() ������ϵ���������Ǹı�x��ֵ���о�һ��A��B��������ʽȡֵ�Ĺ��ɣ�
������ϵ���������Ǹı�x��ֵ���о�һ��A��B��������ʽȡֵ�Ĺ��ɣ�
x | -2 | -1 | 0 | 1 | 2 | 3 |
| 10 | 5 | 2 | 1 | 5 | |
| 17 | 10 | 5 |
��1������ϱ���
��2���۲������Է��֣�
��x=mʱ��![]() ����x=m+1ʱ��
����x=m+1ʱ��![]() �����ǰ����������Ϊ����ʽA���մ���ʽBȡֵ�Ӻ�ʱ�Ӻ�ֵΪ1��
�����ǰ����������Ϊ����ʽA���մ���ʽBȡֵ�Ӻ�ʱ�Ӻ�ֵΪ1��
��������ʽD���մ���ʽBȡֵ�Ӻ���Ӧ���Ӻ�ֵΪ2�������ʽD��
����֪����ʽ![]() ���մ���ʽ
���մ���ʽ![]() ȡֵ�Ӻ���ֱ��д��b-c��ֵ��________��
ȡֵ�Ӻ���ֱ��д��b-c��ֵ��________��
����Ŀ��һ����Ͷ�����Թ涨������Ϊ![]() �֣��ɼ��ﵽ
�֣��ɼ��ﵽ![]() �ּ�����Ϊ�ϸɼ��ﵽ
�ּ�����Ϊ�ϸɼ��ﵽ![]() �ּ�����Ϊ���㣮�ס��������
�ּ�����Ϊ���㣮�ס��������![]() ��ѧ����ij�β��Գɼ����£�
��ѧ����ij�β��Գɼ����£�
�ɼ����֣� |
|
|
|
|
|
|
|
|
|
|
���飨�ˣ� |
|
|
|
|
|
|
|
|
|
|
���飨�ˣ� |
|
|
|
|
|
|
|
|
|
|
![]() �벹���������ijɼ���������
�벹���������ijɼ���������
ͳ���� | ƽ���� | ���� | ��λ�� | �ϸ��� | ������ |
���� |
|
|
|
| ________ |
���� | ________ |
| ________ |
|
|
![]() ����Ϊ�ס���������һ���Ͷ���ɼ��Ϻã���д������֧����Ĺ۵�����ɣ�
����Ϊ�ס���������һ���Ͷ���ɼ��Ϻã���д������֧����Ĺ۵�����ɣ�