Question

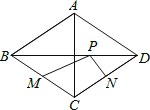
【题目】如图，四边形ABCD中，E、F、G、H依次是各边中点，O是形内一点，若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为6、7、8，四边形DHOG面积为（ ）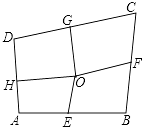
A.6
B.7
C.8
D.9

Answer 1

【答案】B
【解析】解：连接OC，OB，OA，OD， ∵E、F、G、H依次是各边中点，
∴△AOE和△BOE等底等高，所以S△OAE=S△OBE ，
同理可证，S△OBF=S△OCF ， S△ODG=S△OCG ， S△ODH=S△OAH ，
∴S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE ，
∵S四边形AEOH=6，S四边形BFOE=7，S四边形CGOF=8，
∴6+8=7+S四边形DHOG ，
解得S四边形DHOG=7．
故选：B．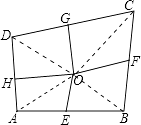

【考点精析】掌握三角形的面积是解答本题的根本，需要知道三角形的面积=1/2×底×高．