题目内容
【题目】如图，正方形ABCD，动点E在AC上，AF⊥AC，垂足为A，AF=AE．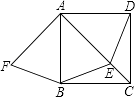 
（1）求证：BF=DE；
（2）当点E运动到AC中点时（其他条件都保持不变），问四边形AFBE是什么特殊四边形？说明理由．
【答案】
（1）证明：∵正方形ABCD，
∴AB=AD，∠BAD=90°，
∵AF⊥AC，
∴∠EAF=90°，
∴∠BAF=∠EAD，
在△ADE和△ABF中
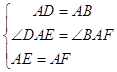
∴△ADE≌△ABF（SAS），
∴BF=DE
（2）解：当点E运动到AC的中点时四边形AFBE是正方形，
理由：∵点E运动到AC的中点，AB=BC，
∴BE⊥AC，BE=AE= 
AC，
∵AF=AE，
∴BE=AF=AE，
又∵BE⊥AC，∠FAE=∠BEC=90°，
∴BE∥AF，
∵BE=AF，
∴得平行四边形AFBE，
∵∠FAE=90°，AF=AE，
∴四边形AFBE是正方形．
【解析】（1）根据正方形的性质判定△ADE≌△ABF后即可得到BF=DE；（2）利用正方形的判定方法判定四边形AFBE为正方形即可．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
