题目内容
（2012•道里区二模）如图，在平面直角坐标系内，点O为坐标原点，直线y=
x+3交x轴于点A，交y轴于点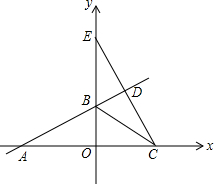
B点C（4，O），过点C作AB的垂CD，点D为垂足，直线CD交y轴于点E，
（1）求点E的坐标．
（2）连接AE，动点P从点A出发以1个单位/秒的速度沿AC向终点C运动，过点P作PP1∥CE交AE于点P1，设点P（点P不与点A，C重合时）运动的时间为t秒，PP1的长为y，求y与t之间的函数关系式（直接写出自变量t的取值范围）；
（3）在（2）的条件下，点Q为P1E中点，连接DQ，当t为何值时有
=
？并求出此时同时经过P、O、E三点的圆的面积．
| 1 |
| 2 |
B点C（4，O），过点C作AB的垂CD，点D为垂足，直线CD交y轴于点E，（1）求点E的坐标．
（2）连接AE，动点P从点A出发以1个单位/秒的速度沿AC向终点C运动，过点P作PP1∥CE交AE于点P1，设点P（点P不与点A，C重合时）运动的时间为t秒，PP1的长为y，求y与t之间的函数关系式（直接写出自变量t的取值范围）；
（3）在（2）的条件下，点Q为P1E中点，连接DQ，当t为何值时有
| PP1 |
| DQ |
| 2 |
| 5 |
分析：（1）对于直线y=
x+3，令x=0求出y的值，即为B的纵坐标，确定出B的坐标；令y=0求出x的值，即为A的横坐标，确定出A的坐标，得出OB与OA的长，由C的坐标得出OC的长，由CD垂直于AB，得到一对直角相等，利用等角的余角相等得到一对角相等，再由一对直角相等，利用两对对应角相等的三角形相似可得出△AOB∽△EOC，由相似得比例，将各自的值代入即可求出OE的长，确定出E的坐标；
（2）如图所示，在直角三角形OCE中，由OE与OC的长，利用勾股定理求出CE的长，再由PP′∥CE，得到两对同位角相等，利用两对对应角相等的三角形相似得到△APP′∽△ACE，由相似得比例，将各自的值代入即可得到y与t的函数关系式，并求出此时自变量t的范围即可；
（3）连接EP，P′C，如图所示，由Q、D分别为P′E、CD的中点，得到QD为三角形P′EC的中位线，利用三角形的中位线定理得到QD等于P′C的一半，代入
=
，得出P′C2=25PP′2，过点P′作P′H⊥CA于点H，可得P′H∥EO，利用两直线平行同位角相等得到∠AEO=∠AP′H，进而确定出tan∠AEO=tan∠AP′H=
，在Rt△P′HC中，利用勾股定理列出关系式P′C2=P′H2+CH2，表示出AH与P′H，得到CH=AC-AH，将各自的值代入列出关于t的方程，求出方程的解得到t的值即可；由∠POE为直角，利用直角所对的弦为直径得到PE为△PEO外接圆的直径，由E的坐标求出OE的长，由AC-AP-OC求出OP的长，在直角三角形POE中，利用勾股定理求出PE的长，即为△PEO外接圆的直径，求出半径，利用圆的面积公式即可求出同时经过P、O、E三点的圆的面积．
| 1 |
| 2 |
（2）如图所示，在直角三角形OCE中，由OE与OC的长，利用勾股定理求出CE的长，再由PP′∥CE，得到两对同位角相等，利用两对对应角相等的三角形相似得到△APP′∽△ACE，由相似得比例，将各自的值代入即可得到y与t的函数关系式，并求出此时自变量t的范围即可；
（3）连接EP，P′C，如图所示，由Q、D分别为P′E、CD的中点，得到QD为三角形P′EC的中位线，利用三角形的中位线定理得到QD等于P′C的一半，代入
| PP′ |
| DQ |
| 2 |
| 5 |
| 4 |
| 3 |
解答：解：（1）∵直线y=
x+3与x轴交于A点，与y轴交于B点，
∴A（-6，0），B（0，3），即OA=6，OB=3，
∵C（4，0），
∴OC=4，
∵CD⊥AB，
∴∠ADC=∠EOC=90°，
∵∠BAC+∠ACE=90°，∠OEC+∠ACE=90°，
∴∠BAC=∠OEC，又∠AOB=∠EOC=90°，
∴△AOB∽△EOC，
∴
=
，即
=
，
∴OE=8，即E（0，8）；
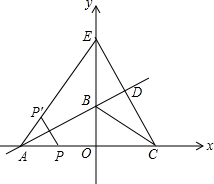
（2）在Rt△OCE中，根据勾股定理得：CE=
=4
，
∵PP′∥CE，
∴△APP′∽△ACE，
∴
=
，
∵PP′=y，AP=t，AC=AO+CO=10，
∴
=
，
则y=
t，自变量t的取值范围为0＜t＜10；
（3）连接EP，P′C，如图所示：
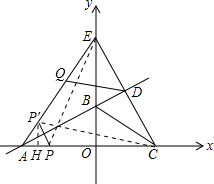
∵Q、D分别为P′E、CD的中点，
∴QD=
P′C，
∵
=
，
∴
=
，
∴
=
，
∴P′C2=25PP′2，
过点P′作P′H⊥CA于点H，可得P′H∥EO，
∴∠AEO=∠AP′H，即tan∠AEO=tan∠AP′H=
，
在Rt△P′HC中，P′C2=P′H2+CH2，
∵tan∠AP′H=
，AP=AP′=t，
∴AH=
t，P′H=
t，
∴CH=AC-AH=10-
t，
∴（
t）2+（10-
t）2=25×（
t）2，
解得：t1=2，t2=-
（不合题意，舍去），
∴当t=2时，
=
；
∵∠POE=90°，
∴PE为△PEO外接圆的直径，
∵E（0，8），即OE=8，OP=AC-AP-OC=10-2-4=4，
∴在Rt△OPE中，根据勾股定理得：PE2=OE2+OP2=80，
∴PE=4
，即△PEO外接圆的半径为2
，
则△PEO外接圆的面积为20π．
| 1 |
| 2 |
∴A（-6，0），B（0，3），即OA=6，OB=3，
∵C（4，0），
∴OC=4，
∵CD⊥AB，
∴∠ADC=∠EOC=90°，
∵∠BAC+∠ACE=90°，∠OEC+∠ACE=90°，
∴∠BAC=∠OEC，又∠AOB=∠EOC=90°，
∴△AOB∽△EOC，
∴
| AO |
| EO |
| BO |
| OC |
| 6 |
| EO |
| 3 |
| 4 |
∴OE=8，即E（0，8）；
（2）在Rt△OCE中，根据勾股定理得：CE=
| OE2+OC2 |
| 5 |
∵PP′∥CE，
∴△APP′∽△ACE，
∴
| PP′ |
| CE |
| AP |
| AC |
∵PP′=y，AP=t，AC=AO+CO=10，
∴
| y | ||
4
|
| t |
| 10 |
则y=
2
| ||
| 5 |
（3）连接EP，P′C，如图所示：
∵Q、D分别为P′E、CD的中点，
∴QD=
| 1 |
| 2 |
∵
| PP′ |
| DQ |
| 2 |
| 5 |
∴
| PP′ | ||
|
| 2 |
| 5 |
∴
| PP′2 |
| P′C2 |
| 1 |
| 25 |
∴P′C2=25PP′2，
过点P′作P′H⊥CA于点H，可得P′H∥EO，
∴∠AEO=∠AP′H，即tan∠AEO=tan∠AP′H=
| 4 |
| 3 |
在Rt△P′HC中，P′C2=P′H2+CH2，
∵tan∠AP′H=
| 4 |
| 3 |
∴AH=
| 3 |
| 5 |
| 4 |
| 5 |
∴CH=AC-AH=10-
| 3 |
| 5 |
∴（
| 4 |
| 5 |
| 3 |
| 5 |
2
| ||
| 5 |
解得：t1=2，t2=-
| 50 |
| 19 |
∴当t=2时，
| PP′ |
| DQ |
| 2 |
| 5 |
∵∠POE=90°，
∴PE为△PEO外接圆的直径，
∵E（0，8），即OE=8，OP=AC-AP-OC=10-2-4=4，
∴在Rt△OPE中，根据勾股定理得：PE2=OE2+OP2=80，
∴PE=4
| 5 |
| 5 |
则△PEO外接圆的面积为20π．
点评：此题属于相似形综合题，涉及的知识有：一次函数与坐标轴的交点，相似三角形的判定与性质，坐标与图形性质，勾股定理，圆周角定理，锐角三角函数定义，以及三角形的中位线定理，熟练掌握性质及定理是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
