题目内容
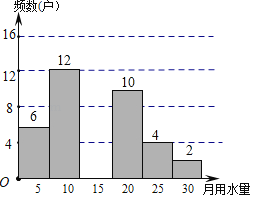
【题目】某校八(1)班学生为了了解某小区家庭月均用水情况,随机调查了该小区部分家庭并将调查数据进行整理,请你根据提供的信息,解答下列问题:
级别 | A | B | C | D | E | F |
月均用水量x(t) | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 | 20<x≤25 | 25<x≤30 |
频数(户) | 6 | 12 | m | 10 | 4 | 2 |
频率 | 0.12 | n | 0.32 | 0.2 | 0.08 | 0.04 |
(1)本次调查采用的方式是 (选填“普查”或“抽样调查”),m= ,n= ;
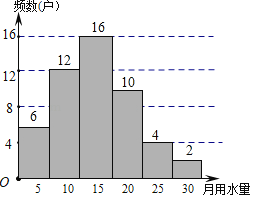
(2)请你补充频数分布直方图;
(3)若将月平均用水量的频数绘制成扇形统计图,则月均用水量15≤x≤20”的圆心角度数是 °;
(4)若该小区共有5000户家庭,求该小区月均用水量超过15t的家庭大约有多少户?
【答案】(1) 抽样调查,16,0.24;(2)见解析;(3)72;(4)大约有1600户.
【解析】
(1)根据调查采用的方式的特征,及频数的求法,即可得到答案;
(2) 由(1)知,得到m,即可补全;
(3) 360°乘以月均用水量15≤x≤20”的占比,即可得到答案;
(4) 超过15t的家庭占比乘以5000,即可得到答案.
解:(1)本次调查采用的方式是抽样调查,
本次调查的户数为:6÷0.12=50(户),
m=50×0.32=16,n=12÷50=0.24,
故答案为:抽样调查,16,0.24;
(2)由(1)知,m=16,
补全的频数分布直方图如右图所示;
(3)月均用水量15≤x≤20”的圆心角度数是:360°×0.2=72°,
故答案为:72;
(4)5000×(0.2+0.08+0.04)=1600(户),
答:该小区月均用水量超过15t的家庭大约有1600户.

【题目】为了解某校八年级学生一门课程的学习情况,小佳和小丽分别对八年级1班和2班本门课程的期末成绩进行了调查分析.小佳对八年级1班全班学生(25名)的成绩进行分析,过程如下收集、整理数据:
表一:
分数段 班级 |
|
|
|
|
八年级1班 | 7 | 5 | 10 | 3 |
表二:
统计量 班级 | 平均数 | 中位数 | 众数 | 极差 | 方差 |
八年级1班 | 78 | 85 | 36 | 105.28 |
小丽用同样的方式对八年级2班全班学生(25名)的成绩进行分析,变数据如下:
统计量 班级 | 平均数 | 中位数 众数 | 极差 | 方差 | |
八年级2班 | 75 | 76 | 73 | 44 | 146.8 |
根据以上信息,解决下列问题:
(1)已知八年级1班学生的成绩处在![]() 这一组的数据如下:
这一组的数据如下:![]() .根据上述数据,将表二补充完整:
.根据上述数据,将表二补充完整:
(2)你认为哪个班级的成绩更为优异?请说明理由
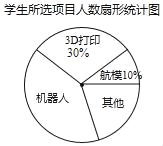
【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.
男、女生所选项目人数统计表
项目 | 男生(人数) | 女生(人数) |
机器人 | 7 | 9 |
3D打印 | m | 4 |
航模 | 2 | 2 |
其他 | 5 | n |
根据以上信息解决下列问题:
(1)m=_____,n=_____;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为_____°;
(3)从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.