题目内容
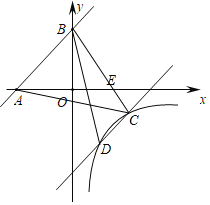
【题目】如图,矩形ABCD中,AC与BD交于点O,AE⊥BD,垂足为E,点F在线段OD上,∠EAO=∠FCB,AE=EF=4,则AD的长为_____.
【答案】4![]()
【解析】
过C点作CM⊥BD于M点,证明∠FCM=∠OCB,借助矩形性质及同角的余角相等,得到∠FCM=∠MCD,从而得到DM=MF=BE,在Rt△ABD中利用射影定理AE2=BEED,可求BE及MF、MD长,在Rt△BMC借助勾股定理求出BC长就是AD的值.
过C点作CM⊥BD于M点,
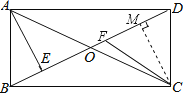
∴EM∥AE,
∴∠MCO=∠EAO.
∵∠EAO=∠FCB,
∴∠MCO=∠FCB,
∴∠MCO﹣∠FCO=∠FCB﹣∠FCO,
即∠FCM=∠OCB.
∵四边形ABCD是矩形,
∴∠OCB=∠OBC.
∵∠OBC+∠BDC=90°,∠MCD+∠MDC=90°,
∴∠OBC=∠MCD.
∴∠MCF=∠MCD.
∴FM=MD.
在△AEB和△CMD中,

∴△AEB和△CMD(AAS).
∴BE=MD.
设BE=MD=MF=x,
在Rt△ABD中,AE⊥BD,
易证△ABE∽△DAE,
∴AE2=BEED,即16=x(4+2x),解得x=2.
∴BM=8.
在Rt△CMB中,利用勾股定理可得BC2=BM2+MC2,
所以BC=![]() .
.
所以AD=BC=4![]() .
.
故答案为:4![]() .
.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,79,81,71,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
|
|
|
|
|
| |
七年级 | 0 | 1 | 0 | a | 7 | 1 |
八年级 | 1 | 0 | 0 | 7 | b | 2 |
分析数据:
平均数 | 众数 | 中位数 | |
七年级 | 78 | 75 |
|
八年级 | 78 |
| 80.5 |
应用数据:
(1)由上表填空:a= ,b= ,c= ,d= .
(2)估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人?
(3)你认为哪个年级的学生对经典文化知识掌握的总体水平较好,请说明理由.
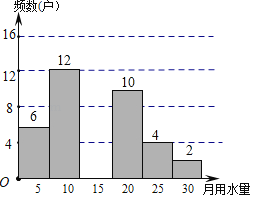
【题目】某校八(1)班学生为了了解某小区家庭月均用水情况,随机调查了该小区部分家庭并将调查数据进行整理,请你根据提供的信息,解答下列问题:
级别 | A | B | C | D | E | F |
月均用水量x(t) | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 | 20<x≤25 | 25<x≤30 |
频数(户) | 6 | 12 | m | 10 | 4 | 2 |
频率 | 0.12 | n | 0.32 | 0.2 | 0.08 | 0.04 |
(1)本次调查采用的方式是 (选填“普查”或“抽样调查”),m= ,n= ;
(2)请你补充频数分布直方图;
(3)若将月平均用水量的频数绘制成扇形统计图,则月均用水量15≤x≤20”的圆心角度数是 °;
(4)若该小区共有5000户家庭,求该小区月均用水量超过15t的家庭大约有多少户?