题目内容
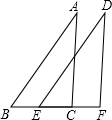 如图,已知:AB=DE,BE=CF,要使△ABC≌△DEF,只需添加一个条件是
如图,已知:AB=DE,BE=CF,要使△ABC≌△DEF,只需添加一个条件是AC=DF
AC=DF
.分析:已知AB=CD,BE=CF,可得BE+EC=CF+EC,即BC=EF,只需添加AC=DF便可利用SSS证明△ABC≌△DEF.
解答:解:应添加条件:AC=DF.
∵BE=CF,
∴BE+EC=CF+EC,即BC=EF,
在△ABC和△DEF中,
∵
,
∴△ABC≌△DEF(SSS).
故答案为:AC=DF.
∵BE=CF,
∴BE+EC=CF+EC,即BC=EF,
在△ABC和△DEF中,
∵
|
∴△ABC≌△DEF(SSS).
故答案为:AC=DF.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
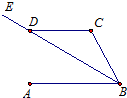 13、如图,已知直线AB∥CD,BE平分∠ABC,交CD于D,∠CDE=150°,则∠C的度数为
13、如图,已知直线AB∥CD,BE平分∠ABC,交CD于D,∠CDE=150°,则∠C的度数为
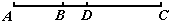
 (2013•温州一模)如图,已知线段AB,
(2013•温州一模)如图,已知线段AB,
 如图,已知线段AB、CD分别表示甲、乙两幢楼的高,AB⊥BD,CD⊥BD,从甲楼顶部A处测得乙楼顶部C的仰角α=30°,测得乙楼底部D的俯角β=60°,已知甲楼高AB=24m,求乙楼CD的高.
如图,已知线段AB、CD分别表示甲、乙两幢楼的高,AB⊥BD,CD⊥BD,从甲楼顶部A处测得乙楼顶部C的仰角α=30°,测得乙楼底部D的俯角β=60°,已知甲楼高AB=24m,求乙楼CD的高.