题目内容
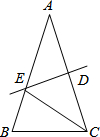 如图,在等腰△ABC中,AB=AC,∠A=30°,线段AC的垂直平分线交AC于D,交AB于E,连接CE,则∠BCE等于( )
如图,在等腰△ABC中,AB=AC,∠A=30°,线段AC的垂直平分线交AC于D,交AB于E,连接CE,则∠BCE等于( )分析:由线段AC的垂直平分线交AC于D,交AB于E,连接CE,可求得∠ACE的度数,又由在等腰△ABC中,AB=AC,∠A=30°,即可求得∠ACB的度数,继而求得答案.
解答:解:∵线段AC的垂直平分线交AC于D,交AB于E,
∴AE=CE,
∴∠ACE=∠A=30°,
∵AB=AC,
∴∠ACB=∠B=
=75°,
∴∠BCE=∠ACB-∠ACE=45°.
故选C.
∴AE=CE,
∴∠ACE=∠A=30°,
∵AB=AC,
∴∠ACB=∠B=
| 180°-∠A |
| 2 |
∴∠BCE=∠ACB-∠ACE=45°.
故选C.
点评:此题考查了线段垂直平分线的性质以及等腰三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
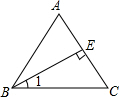 如图,在等腰△ABC中,AB=AC,BE⊥AC,垂足为E,则∠1与∠A的关系式为( )
如图,在等腰△ABC中,AB=AC,BE⊥AC,垂足为E,则∠1与∠A的关系式为( )| A、∠1=∠A | ||
B、∠1=
| ||
| C、∠1=2∠A | ||
| D、无法确定 |
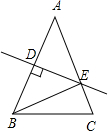 如图,在等腰△ABC中,AB=AC,AB的垂直平分线DE交AB于点D,交另一腰AC于点E,若∠EBC=15°,则∠A=
如图,在等腰△ABC中,AB=AC,AB的垂直平分线DE交AB于点D,交另一腰AC于点E,若∠EBC=15°,则∠A=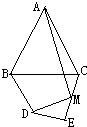 24、如图,在等腰△ABC中,AB=AC,∠ABC=α,在四边形BDEC中,DB=DE,∠BDE=2α,M为CE的中点,连接AM,DM.
24、如图,在等腰△ABC中,AB=AC,∠ABC=α,在四边形BDEC中,DB=DE,∠BDE=2α,M为CE的中点,连接AM,DM.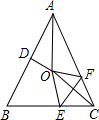 (2012•丽水)如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是
(2012•丽水)如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是 如图,在等腰△ABC中,AB=AC=10cm,直线DE垂直平分AB,分别交AB、AC于D、E两点.若BC=8cm,则△BCE的周长是
如图,在等腰△ABC中,AB=AC=10cm,直线DE垂直平分AB,分别交AB、AC于D、E两点.若BC=8cm,则△BCE的周长是