题目内容
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,延长BC到点F,连接AF,使∠ABC=2∠CAF.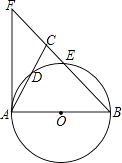
(1)求证:AF是⊙O的切线;
(2)若AC=4,CE:EB=1:3,求CE的长.
【答案】
(1)证明:连接BD,如图1所示:
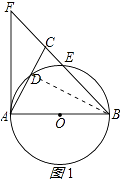
∵AB是⊙O的直径
∴∠ADB=90°,
∵BA=BC,
∴BD平分∠ABC,即∠ABC=2∠ABD
∵∠ABC=2∠CAF,
∴∠ABD=∠CAF,
∵∠ABD+∠CAB=90°,
∴∠CAF+∠CAB=90°,即BA⊥FA,
∴AF是⊙O的切线
(2)解:连接AE,如图2所示:
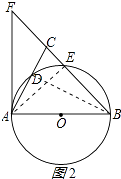
∵AB是⊙O的直径
∴∠AEB=90°,即△AEB为直角三角形,
∵CE:EB=1:3,
设CE长为x,则EB长为3x,BC长为4x.
则AB长为4x,
在Rt△AEB中由勾股定理可得 AE= ![]() ,
,
在Rt△AEC中,AC=4,AE= ![]() ,CE=x,
,CE=x,
由勾股定理得: ![]() ,
,
解得: ![]() ,
,
∵x>0
∴ ![]() ,即CE长为
,即CE长为 ![]() .
.
【解析】(1)连接BD,依据直径所对的圆周角为90°可得到∠ADB=90°,然后由等角对等边的性质以及角平分的定义可得到∠ABC=2∠ABD,于是∠ABD=∠CAF,然后可得到∠CAF+∠CAB=90°,即BA⊥FA;
(2)连接AE,由依据直径所对的圆周角为90°得到∠AEB=90°,设CE长为x,则EB长为3x,AB=BC=4x.由勾股定理可得AE的长,最后,在Rt△AEC中,依据勾股定理列方程求解即可.
【考点精析】本题主要考查了切线的判定定理的相关知识点,需要掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能正确解答此题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目