题目内容
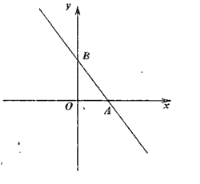
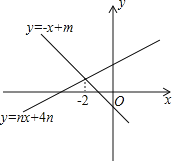
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,依次作正方形
,依次作正方形![]() 、正方形
、正方形![]() 、……正方形
、……正方形![]() ,使得点
,使得点![]() 、…,
、…,![]() 在直线
在直线![]() 上,点
上,点![]() 在
在![]() 轴上,则点
轴上,则点![]() 的坐标是________
的坐标是________
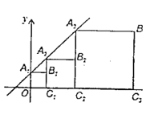
【答案】(22019-1,22018)
【解析】
先求出直线y=x+1与y轴的交点坐标即可得出A1的坐标,故可得出OA1的长,根据四边形A1B1C1O是正方形即可得出B1的坐标,再把B1的横坐标代入直线y=x+1即可得出A1的坐标,同理可得出B2,B3的坐标,可以得到规律:Bn(2n-1,2n-1),据此即可求解点B2019的坐标.
解:∵令x=0,则y=1,
∴A1(0,1),
∴OA1=1.
∵四边形A1B1C1O是正方形,
∴A1B1=1,
∴B1(1,1).
∵当x=1时,y=1+1=2,
∴B2(3,2);
同理可得,B3(7,4);
∴B1的纵坐标是:1=20,B1的横坐标是:1=21-1,
∴B2的纵坐标是:2=21,B2的横坐标是:3=22-1,
∴B3的纵坐标是:4=22,B3的横坐标是:7=23-1,
∴Bn的纵坐标是:2n-1,横坐标是:2n-1,
则Bn(2n-1,2n-1),
∴点B2019的坐标是(22019-1,22018).
故答案为:(22019-1,22018).

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
【题目】2019年4月23日是第24个世界读书日.为了推进中华传统文化教育,营造浓郁的读书氛围,某校举办了“让读书成为习惯,让书香飘满校园”主题活动,为此特为七年级两个班级订购了一批新的图书.七年级两个班级订购图书的情况如下表:

四大名著/套 | 老舍文集/套 | 总费用/元 | |
七年级(1)班 | 2 | 4 | 460 |
七年级(2)班 | 3 | 2 | 530 |
(1)求四大名著和老舍文集每套各是多少元?
(2)学校准备再购买四大名著和老舍文集共10套,总费用不超过800元,求学校最多能买几套四大名著?