题目内容
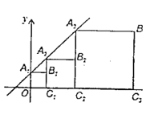
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,点
,点![]() 。
。
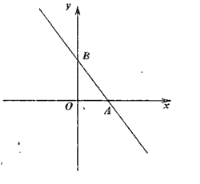
(1)求点![]() 和点
和点![]() 的坐标;
的坐标;
(2)若点![]() 在
在![]() 轴上,且
轴上,且![]() 求点
求点![]() 的坐标。
的坐标。
(3)在![]() 轴是否存在点
轴是否存在点![]() ,使三角形
,使三角形![]() 是等腰三角形,若存在。请求出点
是等腰三角形,若存在。请求出点![]() 坐标,若不存在,请说明理由。
坐标,若不存在,请说明理由。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)在
;(3)在![]() 轴上存在点
轴上存在点![]()
![]()
![]() 使
使![]() 为等腰三角形
为等腰三角形
【解析】
(1)分别代入y=0,x=0,求出与之对应的x,y值,进而可得出点A,B的坐标;
(2)由三角形的面积公式结合S△BOP=![]() S△AOB,可得出OP=
S△AOB,可得出OP=![]() OA,进而可得出点P的坐标;
OA,进而可得出点P的坐标;
(3)由OA,OB的长可求出AB的长,分AB=AM,BA=BM,MA=MB三种情况,利用等腰三角形的性质可求出点M的坐标.
解:(1)当y=0时,-2x+4=0,解得:x=2,
∴点A的坐标为(2,0);
当x=0时,y=-2x+4=4,
∴点B的坐标为(0,4).
(2))∵点P在x轴上,且S△BOP=![]() S△AOB,
S△AOB,
∴OP=![]() OA=1,
OA=1,
∴点P的坐标为(-1,0)或(1,0).
(3))∵OB=4,OA=2,
∴AB= ![]()
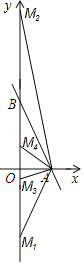
分三种情况考虑(如图所示):
①当AB=AM时,OM=OB=4,
∴点M1的坐标为(0,-4);
②当BA=BM时,BM=2![]() ,
,
∴点M2的坐标为(0,4+2![]() ),点M3的坐标为(0,4-2
),点M3的坐标为(0,4-2![]() );
);
③当MA=MB时,设OM=a,则BM=AM=4-a,
∴AM2=OM2+OA2,即(4-a)2=a2+22,
∴a=![]() ,
,
∴点M4的坐标为(0,![]() ).
).
综上所述:在y轴上存在点M,使三角形MAB是等腰三角形,点M坐标为(0,-4),(0,4+2![]() ),(0,4-2
),(0,4-2![]() )和(0,
)和(0,![]() ).
).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目