Question

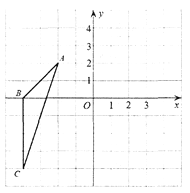
【题目】如图，在平面直角坐标系中，△ABC的顶点坐标分别为A(－2，2)，B(－4，0)，C(－4；－4)，

（1）在y轴右侧，以O为位似中心，画出△A'B'C′，使它与△ABC的相似比为1:2；

（2）根据(1)的作图，sin∠A'C'B′＝__________.

Answer 1

【答案】（1）画图见解析；（2）

【解析】

（1）根据题意可得OA= 2OA' ，OB=2OB'，OC=2OC′，再以原点O为位似中心求得点A'，B'，C′的坐标，然后描点连线即可；

（2）利用勾股定理得出各边长，再利用锐角三角函数关系求出答案即可.

（1）根据题意可得A'（1，-1），B'（2，0），C′（2，2），

如图：

；

（2）如图所示，

∵A'C′==，

∴sin∠A'C'B′＝=．