题目内容
【题目】如图，已知△ABC中，点D在边BC上，∠DAB＝∠B，点E在边AC上，满足AE·CD＝AD·CE.
(1)求证：DE∥AB；
(2)如果点F是DE延长线上一点，且BD是DF和AB的比例中项，连接AF.求证：DF＝AF.
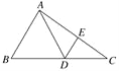
【答案】（1）见解析；（2）见解析.
【解析】
(1)根据已知条件得到
,根据等腰三角形的判定定理得到AD＝BD ,等量代换即可得到结论;
(2)由BD是DF和AB的比例中项,得到BD2＝DF·AB ,等量代换得到AD2＝DF·AB ,推出
,根据相似三角形的性质得到
,于是得到结论.
证明 (1)∵AE·CD＝AD·CE，
∴
＝
，
∵∠DAB＝∠B，
∴AD＝BD，
∴＝
，
∴DE∥AB；
(2)∵BD是DF和AB的比例中项，
∴BD2＝DF·AB，
∵AD＝BD，
∴AD2＝DF·AB，
∴
＝
＝1，
∵DE∥AB，
∴∠ADF＝∠BAD，
∴△ADF∽△DBA，
∴
＝
，
∴DF＝AF.
练习册系列答案
相关题目
