��Ŀ����
����Ŀ��Ϊ��������ͨ�У�ij�㳡�ƻ����½�Ϊ30�㣬�³�Ϊ60��б��AB���и��죬��б���е�D����ȥ�������壨��Ӱ��ʾ������һ��ƽ����ˮƽ��CA��ƽ̨DE��һ���µ�б��BE��
��1��������б��BE���½�Ϊ36�㣬��ƽ̨DE�ij�ԼΪ�����ף�
��2���ھ����½�A��27��Զ��G�����̳���¥��С����D������¥����H ������Ϊ30�㣬��ô��¥GH��ԼΪ�����ף������ȡ�������ο����ݣ�sin36��=0.6��cos36��=0.8��tan36��=0.7�� ![]() =1.7��
=1.7��
���𰸡�
��1���⣺������б��BE���½ǣ�����BEF��Ϊ36�㣬
���BEF=36�㣬
�ߡ�DAC=��BDF=30�㣬AD=BD=30��
��BF= ![]() BD=15��DF=15
BD=15��DF=15 ![]() ��25.98��
��25.98��
EF= ![]() =
= ![]() ��21.43
��21.43
�ʣ�DE=DF��EF=4���ף���
��2���⣺����D��DP��AC������ΪP�� 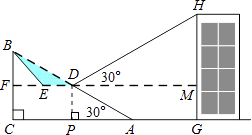
��Rt��DPA��DP= ![]() AD=
AD= ![]() ��30=15��
��30=15��
PA=ADcos30��= ![]() ��30=15
��30=15 ![]() ��
��
�ھ���DPGM�У�MG=DP=15��DM=PG=15 ![]() +27��
+27��
��Rt��DMH��
HM=DMtan30��= ![]() ����15
����15 ![]() +27��=15+9
+27��=15+9 ![]() ��
��
GH=HM+MG=15+15+9 ![]() ��45�ף�
��45�ף�
�𣺽�����GH��ԼΪ45�ף�
����������1����Ϊ����б��BE���½ǣ�����BEF��Ϊ36�㣬�ɡ�DAC=��BDF��AD=BD���õ�BF= ![]() BD��DF��25.98�����ݽ�ֱ��������EF=
BD��DF��25.98�����ݽ�ֱ��������EF= ![]() =
= ![]() ��21.43���õ�DE=DF��EF����2������ʵ������õ�ͼ�Σ���Rt��DPA�У�DP=
��21.43���õ�DE=DF��EF����2������ʵ������õ�ͼ�Σ���Rt��DPA�У�DP= ![]() AD��PA=ADcos30�㣬�ھ���DPGM�У�MG=DP����Rt��DMH�У�HM=DMtan30�㣬�õ�GH=HM+MG.
AD��PA=ADcos30�㣬�ھ���DPGM�У�MG=DP����Rt��DMH�У�HM=DMtan30�㣬�õ�GH=HM+MG.

 �����Ļ�������ҵϵ�д�
�����Ļ�������ҵϵ�д�