题目内容
如图,已知一次函数y=k1x+b(k1≠0)的图象分别与x轴,y轴交于A,B两点,且与反比例函数 (k2≠0)的图象在第一象限的交点为C,过点C作x轴的垂线,垂足为D,若OA=OB=OD=2.
(k2≠0)的图象在第一象限的交点为C,过点C作x轴的垂线,垂足为D,若OA=OB=OD=2.
(1)求一次函数的解析式;
(2)求反比例函数的解析式.
解:(1)∵OA=OB=2,∴A(﹣2,0),B(0,2)。
将A与B的坐标代入y=k1x+b得: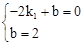 ,解得:
,解得: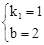 。
。
∴一次函数解析式为y=x+2。
(2)∵OD=2,∴D(2,0)。
∵点C在一次函数y=x+2上,且CD⊥x轴,
∴将x=2代入一次函数解析式得:y=2+2=4,即点C坐标为(2,4)。
∵点C在反比例图象上,∴将C(2,4)代入反比例解析式得:k2=8。
∴反比例解析式为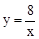 。
。
解析试题分析:(1)由OA与OB的长,确定出A与B的坐标,代入一次函数解析式中求出k1与b的值,即可确定出一次函数解析式。
(2)由OD的长,确定出D坐标,根据CD垂直于x轴,得到C与D横坐标相同,代入一次函数解析式求出C的纵坐标,确定出C坐标,将C坐标代入反比例解析式中求出k2的值,即可确定出反比例解析式。

练习册系列答案
相关题目
青海新闻网讯:西宁市为加大向国家环境保护模范城市大步迈进的步伐,积极推进城市绿地、主题公园、休闲场地建设.园林局利用甲种花卉和乙种花卉搭配成A、B两种园艺造型摆放在夏都大道两侧.搭配数量如下表所示:
| | 甲种花卉(盆) | 乙种花卉(盆) |
| A种园艺造型(个) |  盆 盆 |  盆 盆 |
| B种园艺造型(个) |  盆 盆 |  盆 盆 |
 元.若园林局搭配A种园艺造型
元.若园林局搭配A种园艺造型 个,B种园艺造型
个,B种园艺造型 个共投入
个共投入 元.则A、B两种园艺 造型的单价分别是多少元?
元.则A、B两种园艺 造型的单价分别是多少元?(2)如果搭配A、B两种园艺造型共
 个,某校学生课外小组承接了搭配方案的设计,其中甲种花卉不超过
个,某校学生课外小组承接了搭配方案的设计,其中甲种花卉不超过 盆,乙种花卉不超过
盆,乙种花卉不超过 盆,问符合题意的搭配方案有几种?请你帮忙设计出来.
盆,问符合题意的搭配方案有几种?请你帮忙设计出来. 将二次函数 化为
化为 的形式,下列结果正确的是[( )]
的形式,下列结果正确的是[( )]
A. | B.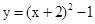 |
C. | D. |
 的图象经过点
的图象经过点 ,且与函数
,且与函数 的图象相交于点
的图象相交于点 .
. 的值;
的值; 轴的交点是B,函数
轴的交点是B,函数 轴的交点是C,求四边形
轴的交点是C,求四边形 的面积(其中O为坐标原点).
的面积(其中O为坐标原点).


 ,点D在线段CA的延长线上,且AD=AB,若反比例函数
,点D在线段CA的延长线上,且AD=AB,若反比例函数 的图象经过点D,求k的值.
的图象经过点D,求k的值.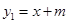 与
与 轴、
轴、 轴分别交于点
轴分别交于点 ,与双曲线
,与双曲线
 分别交于点
分别交于点 ,且
,且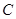 点的坐标为
点的坐标为 .
.
 及双曲线的解析式;
及双曲线的解析式; 的坐标;
的坐标; 在什么范围内取值时,
在什么范围内取值时,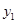 >
> .
.