题目内容
一架长2.5米的梯子,斜立在竖直的墙上,这时梯子的底端距墙底端0.7米,如果梯子的顶底端沿地面远离墙面又滑动了0.8米,梯子的顶端沿墙下滑了多少米?
分析:首先根据题意画出图形可得OB=0.7米,BC=0.8米,AB=2.5米,再利用勾股定理在Rt△ABO中求出AO的值,再在Rt△DOC中计算出DO,再根据AD=AO-DO即可算出AD的值.
解答: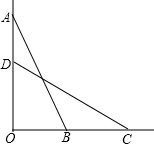 解:如图所示:OB=0.7米,BC=0.8米,AB=2.5米,
解:如图所示:OB=0.7米,BC=0.8米,AB=2.5米,
在Rt△ABO中,
AO=
=
=2.4(米),
∵BO=0.7米,BC=0.8米,
∴CO=1.5米,
在Rt△DOC中:DO2=DC2-OC2,
DO=
=2(米),
∵AO=2.4米,
∴AD=AO-DO=2.4-2=0.4(米).
答:梯子的顶端沿墙下滑了0.4米.
 解:如图所示:OB=0.7米,BC=0.8米,AB=2.5米,
解:如图所示:OB=0.7米,BC=0.8米,AB=2.5米,在Rt△ABO中,
AO=
| AB2-BO2 |
| 6.25-0.49 |
∵BO=0.7米,BC=0.8米,
∴CO=1.5米,
在Rt△DOC中:DO2=DC2-OC2,
DO=
| 2.52-1.52 |
∵AO=2.4米,
∴AD=AO-DO=2.4-2=0.4(米).
答:梯子的顶端沿墙下滑了0.4米.
点评:此题主要考查了勾股定理的应用,关键是熟练掌握勾股定理:直角三角形中,两直角边的平方和等于斜边的平方.

练习册系列答案
相关题目
 如图,一架长2.5米的梯子AB斜靠在竖直的墙AC上,这时B到墙AC的距离为0.7米.
如图,一架长2.5米的梯子AB斜靠在竖直的墙AC上,这时B到墙AC的距离为0.7米. 如图,一架长2.5米的梯子,斜靠在竖直的墙上,这时梯子底端离墙0.7米,为了安装壁灯,梯子顶端离地面2米,请你计算一下,此时梯子底端应再向远离墙的方向拉多远?
如图,一架长2.5米的梯子,斜靠在竖直的墙上,这时梯子底端离墙0.7米,为了安装壁灯,梯子顶端离地面2米,请你计算一下,此时梯子底端应再向远离墙的方向拉多远?