题目内容
 如图,一架长2.5米的梯子,斜靠在竖直的墙上,这时梯子底端离墙0.7米,为了安装壁灯,梯子顶端离地面2米,请你计算一下,此时梯子底端应再向远离墙的方向拉多远?
如图,一架长2.5米的梯子,斜靠在竖直的墙上,这时梯子底端离墙0.7米,为了安装壁灯,梯子顶端离地面2米,请你计算一下,此时梯子底端应再向远离墙的方向拉多远?分析:先在Rt△ABC中根据勾股定理求出AC的长,再在Rt△DCE中利用勾股定理求出CE的长即可解答
解答: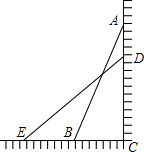 解:在Rt△ABC中,
解:在Rt△ABC中,
∵AB=2.5m,BC=0.7m,
∴AC=
=
=2.4m.
在Rt△DCE中,
∵DE=AB=2.5m,CD=2m,
∴CE=
=
=1.5m.
∴BE=CE-BC=1.5-0.7=0.8m.
答:梯子底端B应再向右拉0.8m.
 解:在Rt△ABC中,
解:在Rt△ABC中,∵AB=2.5m,BC=0.7m,
∴AC=
| AB2-BC2 |
| 2.52-0.72 |
在Rt△DCE中,
∵DE=AB=2.5m,CD=2m,
∴CE=
| DE2-CD2 |
| 2.52-22 |
∴BE=CE-BC=1.5-0.7=0.8m.
答:梯子底端B应再向右拉0.8m.
点评:本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
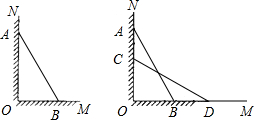 如图,一架长为5米的梯子AB斜靠在与地面OM垂直的墙ON上,梯子底端距离墙ON有3米.
如图,一架长为5米的梯子AB斜靠在与地面OM垂直的墙ON上,梯子底端距离墙ON有3米. 如图,一架长2.5米的梯子AB斜靠在竖直的墙AC上,这时B到墙AC的距离为0.7米.
如图,一架长2.5米的梯子AB斜靠在竖直的墙AC上,这时B到墙AC的距离为0.7米.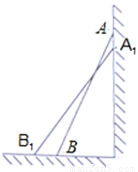
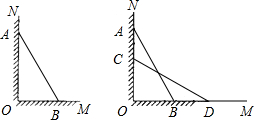 如图,一架长为5米的梯子AB斜靠在与地面OM垂直的墙ON上,梯子底端距离墙ON有3米.
如图,一架长为5米的梯子AB斜靠在与地面OM垂直的墙ON上,梯子底端距离墙ON有3米.