题目内容
 如图,一架长2.5米的梯子AB斜靠在竖直的墙AC上,这时B到墙AC的距离为0.7米.
如图,一架长2.5米的梯子AB斜靠在竖直的墙AC上,这时B到墙AC的距离为0.7米.(1)若梯子的顶端A沿墙AC下滑0.9米至A1处,求点B向外移动的距离BB1的长;
(2)若梯子从顶端A处沿墙AC下滑的距离是点B向外移动的距离的一半,试求梯
子沿墙AC下滑的距离是多少米?
分析:(1)根据题意可知∠C=90°,AB=2.5m,BC=0.7m,根据勾股定理可求出AC的长度,根据梯子顶端B沿墙下滑0.9m,可求出A1C的长度,梯子的长度不变,根据勾股定理可求出B1C的长度,进而求出BB1的长度.
(2)可设点B向外移动的距离的一半为2x,则梯子从顶端A处沿墙AC下滑的距离是x,根据勾股定理建立方程,解方程即可.
(2)可设点B向外移动的距离的一半为2x,则梯子从顶端A处沿墙AC下滑的距离是x,根据勾股定理建立方程,解方程即可.
解答:解:(1)∵AB=2.5m,BC=O.7m,
∴AC=
=2.4m
∴A1C=AC-AA1=2.4-0.9=1.5m,
∴B1C=
=2m,
∴BB1=B1C-BC=0.5m;
(2)梯子从顶端A处沿墙AC下滑的距离是x,则点B向外移动的距离的一半为2x,
由勾股定理得:(2.4-x)2+(0.7+2x)2=2.52,
解得:x=
,
答:梯子沿墙AC下滑的距离是
米.
∴AC=
| 2.52-0.72 |
∴A1C=AC-AA1=2.4-0.9=1.5m,
∴B1C=
| 2.52-1.52 |
∴BB1=B1C-BC=0.5m;
(2)梯子从顶端A处沿墙AC下滑的距离是x,则点B向外移动的距离的一半为2x,
由勾股定理得:(2.4-x)2+(0.7+2x)2=2.52,
解得:x=
| 3 |
| 2 |
答:梯子沿墙AC下滑的距离是
| 3 |
| 2 |
点评:本题考查勾股定理的应用,在直角三角形里根据勾股定理,知道其中两边就可求出第三边,从而可求解.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
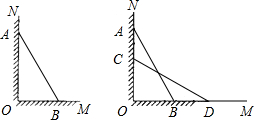 如图,一架长为5米的梯子AB斜靠在与地面OM垂直的墙ON上,梯子底端距离墙ON有3米.
如图,一架长为5米的梯子AB斜靠在与地面OM垂直的墙ON上,梯子底端距离墙ON有3米. 如图,一架长2.5米的梯子,斜靠在竖直的墙上,这时梯子底端离墙0.7米,为了安装壁灯,梯子顶端离地面2米,请你计算一下,此时梯子底端应再向远离墙的方向拉多远?
如图,一架长2.5米的梯子,斜靠在竖直的墙上,这时梯子底端离墙0.7米,为了安装壁灯,梯子顶端离地面2米,请你计算一下,此时梯子底端应再向远离墙的方向拉多远?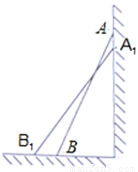
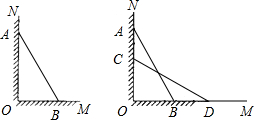 如图,一架长为5米的梯子AB斜靠在与地面OM垂直的墙ON上,梯子底端距离墙ON有3米.
如图,一架长为5米的梯子AB斜靠在与地面OM垂直的墙ON上,梯子底端距离墙ON有3米.