题目内容
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b<0;③a+bm<m(am+b)(m≠1);④(a+c)2<2;⑤a> .其中正确的是( )
.其中正确的是( )

 .其中正确的是( )
.其中正确的是( )
| A.①⑤ | B.①②⑤ | C.②⑤ | D.①③④ |
A.
试题分析:先充分挖掘图象所给出的信息,包括对称轴、开口方向、与坐标轴的交点、顶点位置等,然后根据二次函数图象的性质解题.
从开口方向向上可知a>0,与y轴交点在x轴下方,则C<0,又因为对称轴x=?
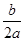 >0,∴b<0,abc>0,①对;0<?
>0,∴b<0,abc>0,①对;0<?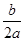 <1,∴-b<2a,∴2a+b>0,②不对;
<1,∴-b<2a,∴2a+b>0,②不对;∵x=1,y1=a+b+c;
∴x=m,y2=am2+mb+c=m(am+b)+c,
当m>1,y2>y1;当m<1,y2<y1,所以不能确定,③不对;
∴(a+c+b)(a+c?b)=(a+b+c)(a?b+c)
x=1,y=a+b+c=0;x=?1,y=a?b+c>0
∴(a+b+c)(a?b+c)=0
∴(a+c)2?b2=0,所以④不对;
∵x=?1,a?b+c=2;x=1,a+b+c=0
∴2a+2c=2,a+c=1,a=1?c=1+(?c)>1,所以选⑤
综上所述:选①⑤,即选A.
考点:二次函数图象与系数的关系.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 与x轴交于A、B两点,与y轴交于点C.
与x轴交于A、B两点,与y轴交于点C.
 图象的一部分,图象过点
图象的一部分,图象过点 (3,0),且对称轴为
(3,0),且对称轴为 ,给出下列四个结论:①
,给出下列四个结论:① ;②
;② ;③
;③ ;④
;④ ,其中正确结论的序号是___________.(把你认为正确的序号都写上)
,其中正确结论的序号是___________.(把你认为正确的序号都写上)
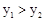 ?
? 的最小值是 .
的最小值是 . 的顶点坐标是 .
的顶点坐标是 . 的图象过(1,-1)和(3,0),则下列关于这个二次函数的描述,正确的是( ).
的图象过(1,-1)和(3,0),则下列关于这个二次函数的描述,正确的是( ).