Question

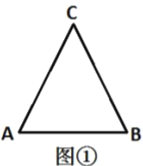
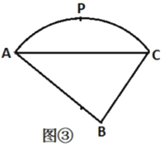
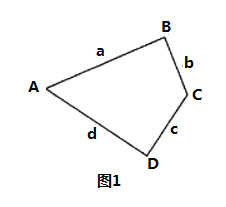
【题目】我们把有一组对角为直角的四边形叫直方形．设这两个直角的夹边长分别为a，b和c，d，记叫直方形的方周长，如图1．

（1）判断与的大小；

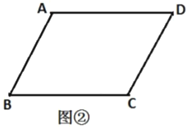
（2）如图2，已知点P为双曲线上一动点，过点P作PA⊥x轴交x轴正半轴于点A，以坐标原点O为圆心、OA长为半径作，点B为上不同于点A的点，当以点P，A，O，B为顶点的直方形的方周长取最小值时，求直方形PAOB的面积；

（3）已知直线：与x轴、y轴相交于点A，B，点P为平面上一点，以点P，A，O，B为顶点的直方形的方周长，当反比例函数的图象与直线有两个交点时，求k的取值范围．

Answer 1

【答案】（1）；（2）；（3）或

【解析】

（1）连接，根据∠B=∠D=90°，利用勾股定理解决问题即可；

（2）由四边形为直方形，可得为的切线，进而得到，得出，再利用二次函数的性质解决问题即可；

（3）由直线l：与x轴，y轴交于点A，B，推出A（1-a，0），B（0，a），可得L2=2[（1-a）2+a2]=50，解得a=-3或4．再分两种情形分别求解即可；

（1）如图，连接，

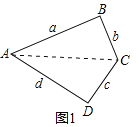
在与中，

∵∠B=∠D=90°，

∴AC2=AB2+BC2=AD2+CD2，

由勾股定理可知，．

（2）四边形为直方形，且，

，则为的切线，

，点的横坐标为且点在双曲线上．

．

．

当时，取得最小值，此时

直方形为正方形，．

（3）直线与轴、轴相交于点，

，．

．

解得：，．

①当时，与有两个交点．

（Ⅰ）当时有两个交点：

（1）当时，与联立得：，有两个不同的解．

，

．

当时有两个不同的解．

由上可知，当或时有两个交点：

②当时，与有两个交点．

（Ⅰ）当时有两个交点：

（Ⅱ）当时，与联立得：，有两个不同的解．

，

．

当时有两个不同的解．

由上可知，当或时有两个交点．

综上所述，当反比例函数的图象与直线有两个交点时，的取值范围是或．