��Ŀ����
����Ŀ�����ⷢ��
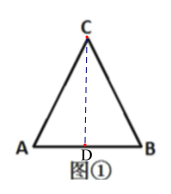
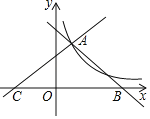
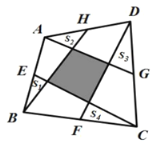
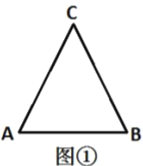
��1����ͼ�٣�![]() Ϊ�߳�Ϊ
Ϊ�߳�Ϊ![]() �ĵȱ������Σ�
�ĵȱ������Σ�![]() ��
��![]() ����һ����
����һ����![]() ƽ��
ƽ��![]() ����������߶�
����������߶�![]() �ij���Ϊ____��
�ij���Ϊ____��
����̽��
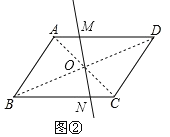
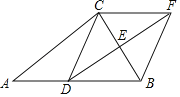
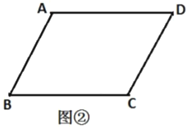
��2����ͼ�ڣ�![]() ��
��![]() ����
����![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() �ϣ���
�ϣ���![]() ƽ��
ƽ��![]() ���������
���������![]() ��̣����㻭������Ҫ����߶�
��̣����㻭������Ҫ����߶�![]() ���������ʱ
���������ʱ![]() ��
��![]() �ij��ȣ�
�ij��ȣ�
������
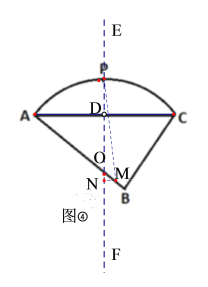
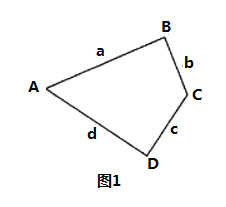
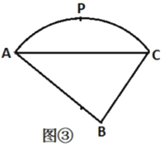
��3����ͼ�ۣ�ij����һ��յ���������·Χ�ɣ����߶�![]() ����֪
����֪![]() �ף�
�ף�![]() �ף�
�ף�![]() ��Բ����
��Բ����![]() ���ϣ��ֹ滮�ڿյ�����ֲ��ƺ����
���ϣ��ֹ滮�ڿյ�����ֲ��ƺ����![]() ���е�
���е�![]() ��һ��ֱ·
��һ��ֱ·![]() (��
(��![]() ��
�� ![]() ��)�������Ƿ����
��)�������Ƿ����![]() ��ʹ��
��ʹ��![]() ƽ�ָÿյص����?�����ڣ��������ʱ
ƽ�ָÿյص����?�����ڣ��������ʱ![]() �ij��ȣ��������ڣ���˵�����ɣ�
�ij��ȣ��������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2��MN=3
����2��MN=3![]() ��AM=2.5����ͼ����⣻��3������
��AM=2.5����ͼ����⣻��3������![]() ��ʹ��
��ʹ��![]() ƽ�ָÿյص������AM= 146���ף���
ƽ�ָÿյص������AM= 146���ף���
��������
��1����CD��AB�ڵ�D�����õȱ����������ߺ�һ�����ʺ�ֱ�������ε��������AD�ij������ɣ�
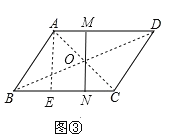
��2������ƽ���ı��ζԽ��ߵĽ����ֱ�߽�ƽ���ı��ε�����ֳ���ȵ������֣���MN��BCʱ��MN��̣���A��AE��BC�ڵ�E���������Ǻ����Ķ��壬��AE�ij�������MN�ij��������EN�ij�����AM�ij���
��3����AC�Ĵ�ֱƽ����EF��AB�ڵ�O����AC�ڵ�D�����OΪ![]() ����Բ��Բ�ģ�ͨ��������Ǻ����Ķ��壬���OD��ֵ���Ӷ���
����Բ��Բ�ģ�ͨ��������Ǻ����Ķ��壬���OD��ֵ���Ӷ���![]() ��
��![]() �����߶�OB��ȡ��M������PM��ʹOPM�����=1050���������OM���������AM��ֵ��Ȼ��õ����ۣ�
�����߶�OB��ȡ��M������PM��ʹOPM�����=1050���������OM���������AM��ֵ��Ȼ��õ����ۣ�
��1����ͼ�٣���CD��AB�ڵ�D��
��![]() Ϊ�߳�Ϊ
Ϊ�߳�Ϊ![]() �ĵȱ������Σ�
�ĵȱ������Σ�
��AD=BD��
��![]() ƽ��
ƽ��![]() �������
�������
��CD=![]() AC=
AC=![]() ��2=
��2=![]() ��
��
�ʴ��ǣ�![]() ��
��
��2������AC��BD���ڵ�O��
����O��ֱ��MN����AD��M����BC��N����ͼ�ڣ�
���ı���ABCDΪƽ���ı��Σ�
��OA=OC��AD��BC��
����CAD=��ACB��
����AOM=��CON��
����AOM�ա�CON��ASA����
��S��AOM=S��CON��
ͬ���ɵã���OMD�ա�ONB����AOB�ա�COD��
��S��OMD=S��ONB��S��AOB=S��COD��
��S��AOM+S��AOB+S��BON=S��CON+S��COD+S��OMD��
����MN���ı���ABCD�ֳ������ȵ������֣�
��MN��BCʱ��MN��̣���ͼ����ʾ��
��A��AE��BC�ڵ�E��
��Rt��ABE��
����ABC=60�㣬
��sin60span>��=![]() ��
��
��AE=![]() ��6=3
��6=3![]() ��
��
��AD��BC��AE��BC��MN��BC��
��MN=AE=3![]() ��
��
���ʱMN�ij���Ϊ3![]() ��
��
��AE��MN��AO=CO��
��EN=CN��
��BE=![]() AB=3��
AB=3��
��CE=BC-BE=8-3=5��
��EN=2.5��
��AD��BC��AE��BC��MN��BC��
���ı���AENM�Ǿ��Σ�����AM=EN=2.5��
��3������![]() ��ʹ��
��ʹ��![]() ƽ�ָÿյص�������������£�
ƽ�ָÿյص�������������£�
��AC�Ĵ�ֱƽ����EF��AB�ڵ�O����AC�ڵ�D�����OΪ![]() ����Բ��Բ�ģ���ͼ�ܣ�
����Բ��Բ�ģ���ͼ�ܣ�
�ߵ�P��![]() ���е㣬
���е㣬
���P��ֱ��EF�ϣ�
��![]() ���ף���
���ף���![]() ���ף���
���ף���![]() ��
��
��AC=![]() =200���ף���AD=
=200���ף���AD=![]() AC=100���ף���
AC=100���ף���
��tan��BAC=![]() ��
��
��OD=![]() AD=75���ף���
AD=75���ף���
��![]() ��ƽ���ף���
��ƽ���ף���
��![]() ��ƽ���ף���
��ƽ���ף���
��![]() ��ƽ���ף���
��ƽ���ף���
��ͼ��OBCP�������ͼ��AOP�������2100ƽ���ף�
�����߶�OB��ȡ��M������PM��ʹOPM�����=1050��ƽ���ף������ɣ�
��sin��BAC=![]() ��
��
��OA=![]() OD=
OD=![]() ��75=125���ף���
��75=125���ף���
��OP=OA=125���ף���
����M��MN��EF�ڵ�N��
��![]() OPMN=1050������MN=2100��125=
OPMN=1050������MN=2100��125=![]() ���ף���
���ף���
��MN��AC��
��AOD~MON��
��![]() ������
������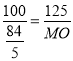 ����ã�MO=21���ף���
����ã�MO=21���ף���
��AM=AO+MO=125+21=146���ף���
��AM��AB��
�����![]() ��ʹ��
��ʹ��![]() ƽ�ָÿյص��������ʱ��AM= 146���ף���
ƽ�ָÿյص��������ʱ��AM= 146���ף���