Question

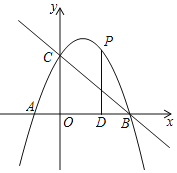
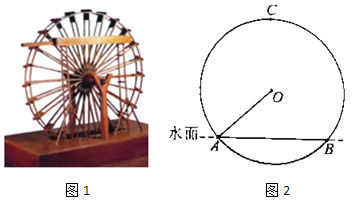
【题目】筒车是我国古代发明的一种水利灌溉工具.如图1，明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理.如图2，筒车盛水桶的运行轨迹是以轴心O为圆心的圆.已知圆心在水面上方，且圆被水面截得的弦AB长为6米，∠OAB=41.3°，若点C为运行轨道的最高点（C，O的连线垂直于AB），求点C到弦AB所在直线的距离.（参考数据：sin41.3°≈0.66，cos41.3°≈0.75，tan41.3°≈0.88）

Answer 1

【答案】6.64米

【解析】

通过垂径定理求出AD，再通过三角函数解直角三角形，求出AO和OD的值，从而得到点C到弦AB所在直线的距离.

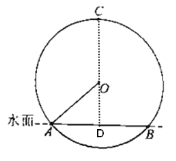
解：如图：连接CO并延长，交AB于点D，

∵OD⊥AB，AB=6，

∴AD=AB=3，

在Rt△OAD中, ∠OAB=41.3°，cos∠OAD=，

∴AO=，

∵tan∠OAD=,

∴OD=AO·tan∠OAD=2.64，

∴CD=OC+OD=AO+OD=4+2.64=6.64米，

答：点C到弦AB所在直线的距离是6.64米.