题目内容
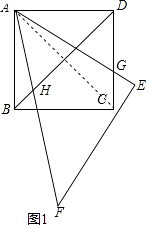
【题目】如图,已知正方形ABCD,将一块等腰直角三角板的锐角顶点与A重合,并将三角板绕A点旋转,如图1,使它的斜边与BD交于点H,一条直角边与CD交于点G.
(1)请适当添加辅助线,通过三角形相似,求出 ![]() 的值;
的值;
(2)连接GH,判断GH与AF的位置关系,并证明;
(3)如图2,将三角板旋转至点F恰好在DC的延长线上时,若AD=3 ![]() ,AF=5
,AF=5 ![]() .求DG的长.
.求DG的长.
【答案】
(1)
解:连接AC,
∵四边形ABCD是正方形,
∴∠BAC=∠ABD=∠ACD=45°,cos∠BAC=cos45°= ![]() ,
,
又∵△AEF是等腰直角三角形,
∴∠EAF=45°,
∴∠BAH+∠FAC=∠FAC+∠EAC=45°,
∴∠BAH=∠EAC,
∴△BAH∽△ACG,
∴ ![]() =
= ![]() =
= ![]() ;
;
(2)
解:GH⊥AF,理由如下:
∵在Rt△AEF中,cos∠EAF=cos45°= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
又∵∠HAG=∠EAF
∴△HAG∽△EAF,
∴∠AHG=∠E=90°,
∴GH⊥AF;
(3)
解:∵在Rt△AGH中,sin∠GAH=sin45°= ![]() =
= ![]() ,
,
∴AG= ![]() GH,
GH,
又∵∠ADG=∠E=90°,∠AGD=∠FGE,
∴△AGD∽△FGE,
∴ ![]() =
= ![]() =
= ![]() ,
,
又∵在Rt△AEF中,AF=5 ![]() ,
,
∴EF=5,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴可设GH为3x,则GF=5x,FH= ![]() =4x,
=4x,
∴AF=AH+FH=3x+4x=5 ![]() ,
,
∴x= ![]() ,
,
∴AG= ![]() GH=
GH= ![]() ×3×
×3× ![]() =
= ![]() ,
,
∴GE=AE﹣AG=5﹣ ![]() =
= ![]() ,
,
又∵ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴DG= ![]() .
.
【解析】(1)连接AC,根据正方形的性质的∠BAC=∠ABP=∠ABP=45°,cos∠BAC=cos45°= ![]() ,根据等腰直角三角形的性质得到∠EAF=45°,根据相似三角形的性质即可得到结论;(2)根据三角函数的定义得到
,根据等腰直角三角形的性质得到∠EAF=45°,根据相似三角形的性质即可得到结论;(2)根据三角函数的定义得到 ![]() =
= ![]() =
= ![]() ,根据相似三角形的性质即可得到结论;(3)根据三角函数的定义得到AG=
,根据相似三角形的性质即可得到结论;(3)根据三角函数的定义得到AG= ![]() GH,根据相似三角形的性质得到
GH,根据相似三角形的性质得到 ![]() =
= ![]() =
= ![]() ,设GH为3x,则GF=5x,根据勾股定理得到FH=
,设GH为3x,则GF=5x,根据勾股定理得到FH= ![]() =4x,得到AG=
=4x,得到AG= ![]() GH=
GH= ![]() ×3×
×3× ![]() =
= ![]() ,于是得到结论.
,于是得到结论.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对正方形的性质的理解,了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.










