Question

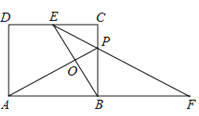
【题目】如图，在平面直角坐标系中，抛物线与轴相交于点，，与轴相交于点，点为抛物线的顶点，轴于点，且．

（1）求抛物线的解析式；

（2）做点与点关于对称轴对称，连接，过点作，过点作，与相交于点，若，求点的坐标；

（3）在（2）的条件下，点是第一象限内抛物线上一点，连接与相交于点，过点做轴于点，与相交于，连接，若，求点的坐标和的值．

Answer 1

【答案】（1）；（2）；（3），

【解析】

（1）首先根据抛物线解析式变换形式得出A、B两点坐标，进而得出DE，再转换成顶点式，即可得出抛物线解析式；

（2）根据对称以及矩形的性质，通过等量互换，即可判定，进而得出F点坐标；

（3）首先通过等角互换得出，然后利用坐标构建方程即可得出点P坐标，再利用三角函数进行转化即可得出的值.

（1）∵，令

解得，，

∴

∵，

∴，

，

∴，

解得

∴；

（2）过作轴于，

∵、关于对称，

∴，

∵四边形为矩形，

∴，

又∵，

∴，

∵，

∴，

∵，

∴，

∴，

又∵，，

∴，

∴．

∴；

（3）∵，

∴，

∵，

∴，

∴，

作交于，则

∴，

∴，

设，则，，

∴，

设，则，

，

∵，

∴

∴，（舍去）

∴

中：

，

∵，

∴

中：，，

，

作于，中：，，

，，

中：