题目内容
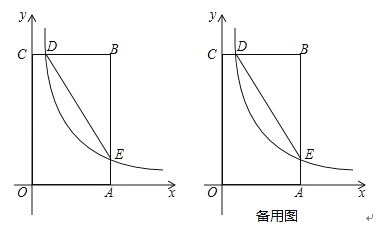
【题目】已知:⊙O上两个定点A,B和两个动点C,D,AC与BD交于点E.
(1)如图1,求证:EAEC=EBED
(2)如图2,若![]() , AD是⊙O的直径,求证:ADAC=2BDBC
, AD是⊙O的直径,求证:ADAC=2BDBC
(3)如图3,若AC⊥BD,点O到AD的距离为2,求BC的长
【答案】
(1)
证明:∵∠EAD=∠EBC,∠BCE=∠ADE,
∴△AED∽△BEC,
∴![]() =
=![]() ,
,
∴EAEC=EBED
(2)
证明:如图2,

连接CD,OB交AC于点F
∵B是弧AC的中点,
∴∠BAC=∠ADB=∠ACB,且AF=CF=0.5AC.
又∵AD为⊙O直径,
∴∠ABC=90°,又∠CFB=90°.
∴△CBF∽△ABD.
∴![]() ,故CFAD=BDBC.
,故CFAD=BDBC.
∴ACAD=2BDBC
(3)
解:如图3,连接AO并延长交⊙O于F,连接DF,

∴AF为⊙O的直径,
∴∠ADF=90°,
过O作OH⊥AD于H,
∴AH=DH,OH∥DF,
∵AO=OF,
∴DF=2OH=4,
∵AC⊥BD,
∴∠AEB=∠ADF=90°,
∵∠ABD=∠F,
∴△ABE∽△ADF,
∴∠1=∠2,
∴![]()
∴BC=DF=4.
【解析】(1)根据同弧所对的圆周角相等得到角相等,从而证得三角形相似,于是得到结论;
(2)如图2,连接CD,OB交AC于点F由B是弧AC的中点得到∠BAC=∠ADB=∠ACB,且AF=CF=0.5AC.证得△CBF∽△ABD.即可得到结论;
(3)如图3,连接AO并延长交⊙O于F,连接DF得到AF为⊙O的直径于是得到∠ADF=90°,过O作OH⊥AD于H,根据三角形的中位线定理得到DF=2OH=4,通过△ABE∽△ADF,得到1=∠2,于是结论可得.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目