题目内容
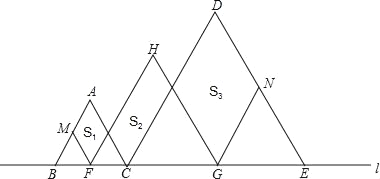
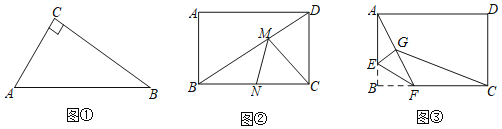
【题目】如图，在等腰三角形ABC中，∠BAC=120°，AB=AC=2，点D是BC边上的一个动点（不与B、C重合），在AC上取一点E，使∠ADE=30°．
（1）求证：△ABD∽△DCE；
（2）设BD=x，AE=y，求y关于x的函数关系式并写出自变量x的取值范围．
【答案】（1）答案见解析；（2）
（0＜x＜
）．
【解析】试题分析：（1）根据两角相等得到△ABD∽△DCE；
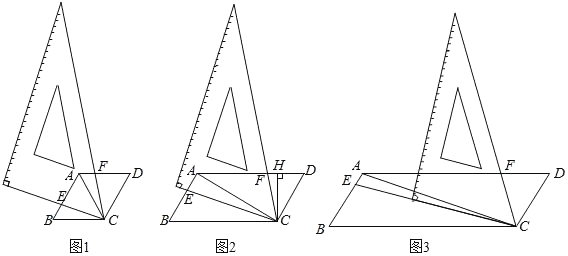
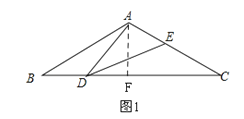
（2）如图1，作高AF，根据直角三角形30°的性质求AF的长，根据勾股定理求BF的长，则可得BC的长，根据（1）中的相似列比例式可得函数关系式，并确定取值．
（1）∵△ABC是等腰三角形，且∠BAC=120°，∴∠ABD=∠ACB=30°，∴∠ABD=∠ADE=30°，∵∠ADC=∠ADE+∠EDC=∠ABD+∠DAB，∴∠EDC=∠DAB，∴△ABD∽△DCE；
（2）如图1，∵AB=AC=2，∠BAC=120°，过A作AF⊥BC于F，∴∠AFB=90°，∵AB=2，∠ABF=30°，∴AF=
AB=1，∴BF=
，∴BC=2BF=
，则DC=
﹣x，EC=2﹣y，∵△ABD∽△DCE，∴
，∴
，化简得： 
（0＜x＜
）．
【题目】有这样一个问题，探究函数y＝x2﹣2
的图象与性质，小张根据学习函数的经验，对函数y＝x2﹣2的图象与性质进行了研究，下面是小张的探究过程，请补充完整：
（1）函数y＝x2﹣2的自变量取值范围是 ．
（2）下表是y与x的几组对应值：
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | |
y | … | n | 3 | 0 | ﹣1 | 0 | ﹣1 | 0 | 3 | m |
求m的值；
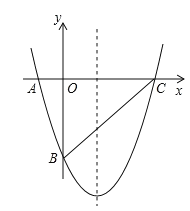
（3）如图，在平面直角坐标系xOy中，算出了以上表中各对对应值为坐标的点，根据算出的点，画出该函数的图象；
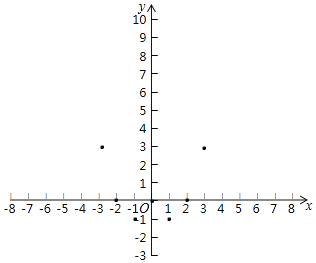
（4）进一步探究发现，该函数图象在第四象限内的最低点是1，﹣1），结合函数的图象，写出该函数的其他性质（一条即可）；
（5）根据图象回答：方程x2﹣2＝﹣
有 个实数解．
