题目内容
如图,在△ABC中,AB=AC,AB=8,BC=12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是______.


连接AD,
∵AB=AC,AB=8,BC=12,以AB、AC为直径作半圆,
∴∠ADB=∠ADC=90°,即AD⊥BC,
∴BD=CD=6,
∴AD⊥BC,
∴AD=
=
=2
,
∴S△ABC=
×AD×BC=
×2
×12=12
,
∵图中阴影部分的面积是:圆的面积-S△ABC=π×42-12
=16π-12
.
故答案为:16π-12
.
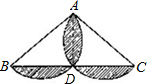
∵AB=AC,AB=8,BC=12,以AB、AC为直径作半圆,
∴∠ADB=∠ADC=90°,即AD⊥BC,
∴BD=CD=6,
∴AD⊥BC,
∴AD=
| AC2-CD2 |
| 64-36 |
| 7 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 7 |
∵图中阴影部分的面积是:圆的面积-S△ABC=π×42-12
| 7 |
| 7 |
故答案为:16π-12
| 7 |


练习册系列答案
相关题目