题目内容
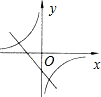
如图,直线y=﹣2x+2与x轴、y轴分别交于A、B两点,将△OAB绕点O逆时针方向旋转90°后得到△OCD.
(1)填空:点C的坐标是( , ),点D的坐标是( , );
(2)设直线CD与AB交于点M,求线段BM的长;
(3)在y轴上是否存在点P,使得△BMP是等腰三角形?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由.

(1)填空:点C的坐标是( , ),点D的坐标是( , );
(2)设直线CD与AB交于点M,求线段BM的长;
(3)在y轴上是否存在点P,使得△BMP是等腰三角形?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由.

(1)点C的坐标是(0,1),点D的坐标是(﹣2,0)
(2)
 .
.
(3)存在,所有满足条件的点P的坐标是P1(0,2+
 )、P2(0,2﹣
)、P2(0,2﹣
 )、P3(0,
)、P3(0, )、P4(0,
)、P4(0, ).
).
(2)

 .
.(3)存在,所有满足条件的点P的坐标是P1(0,2+

 )、P2(0,2﹣
)、P2(0,2﹣
 )、P3(0,
)、P3(0, )、P4(0,
)、P4(0, ).
).解:(1)y=﹣2x+2,
当x=0时,y=2,
当y=0时,x=1
,∴A(1,0),B(0,2),
∵将△OAB绕点O逆时针方向旋转90°后得到△OCD,
∴OC=0A=1,OD=OB=2,
∴点C的坐标是(0,1),点D的坐标是(﹣2,0),
故答案为:0,1,﹣2,0.
(2)由(1)可知:CD= =
= ,BC=1,
,BC=1,
又∠ABO=∠ADC,∠BCM=∠DCO
∴△BMC∽△DOC(有两角对应相等的两三角形相似),
∴ =
= ,
,
即 =
= ,
,
∴BM= =
=
 ,
,
答:线段BM的长是
 .
.
(3)存在,
分两种情况讨论:
①以BM为腰时,
∵BM=
 ,又点P在y轴上,且BP=BM,
,又点P在y轴上,且BP=BM,
此时满足条件的点P有两个,它们是P1(0,2+
 )、P2(0,2﹣
)、P2(0,2﹣
 ),
),
过点M作ME⊥y轴于点E,
∵∠BMC=90°,则△BME∽△BCM,
∴ =
= ,
,
∴BE= =
= ,
,
又∵BM=PM,
∴PE=BE= ,
,
∴BP= ,
,
∴OP=2﹣ =
= ,
,
此时满足条件的点P有一个,它是P3(0, ),
),

②以BM为底时,作BM的垂直平分线,分别交y轴、BM于点P、F,
由(2)得∠BMC=90°,
∴PF∥CM,
∵F是BM的中点,
∴BP= BC=
BC= ,
,
∴OP=OB﹣BP=2﹣ =
= ,
,
此时满足条件的点P有一个,它是P4(0, ),
),
综上所述,符合条件的点P有四个,
它们是:P1(0,2+
 )、P2(0,2﹣
)、P2(0,2﹣
 )、P3(0,
)、P3(0, )、P4(0,
)、P4(0, ).
).
答:存在,所有满足条件的点P的坐标是P1(0,2+
 )、P2(0,2﹣
)、P2(0,2﹣
 )、P3(0,
)、P3(0, )、P4(0,
)、P4(0, ).
).

(1)把x=0,y=0分别代入解析式求出A、B的坐标,即可得出C、D的坐标;
(2)根据勾股定理求出CD,证△BMC∽△DOC,得到比例式即可求出答案;
(3)有两种情况:①以BM为腰时,满足BP=BM的有两个;过点M作ME⊥y轴于点E,证△BME∽△BCM,求出BE、PE,进一步求出OP即可;②以BM为底时,作BM的垂直平分线,分别交y轴、BM于点P、F,根据等腰三角形的性质求出即可.
当x=0时,y=2,
当y=0时,x=1
,∴A(1,0),B(0,2),
∵将△OAB绕点O逆时针方向旋转90°后得到△OCD,
∴OC=0A=1,OD=OB=2,
∴点C的坐标是(0,1),点D的坐标是(﹣2,0),
故答案为:0,1,﹣2,0.
(2)由(1)可知:CD=
 =
= ,BC=1,
,BC=1,又∠ABO=∠ADC,∠BCM=∠DCO
∴△BMC∽△DOC(有两角对应相等的两三角形相似),
∴
 =
= ,
,即
 =
= ,
,∴BM=
 =
=
 ,
,答:线段BM的长是

 .
. (3)存在,
分两种情况讨论:
①以BM为腰时,
∵BM=

 ,又点P在y轴上,且BP=BM,
,又点P在y轴上,且BP=BM,此时满足条件的点P有两个,它们是P1(0,2+

 )、P2(0,2﹣
)、P2(0,2﹣
 ),
),过点M作ME⊥y轴于点E,
∵∠BMC=90°,则△BME∽△BCM,
∴
 =
= ,
,∴BE=
 =
= ,
,又∵BM=PM,
∴PE=BE=
 ,
,∴BP=
 ,
,∴OP=2﹣
 =
= ,
,此时满足条件的点P有一个,它是P3(0,
 ),
),
②以BM为底时,作BM的垂直平分线,分别交y轴、BM于点P、F,
由(2)得∠BMC=90°,

∴PF∥CM,
∵F是BM的中点,
∴BP=
 BC=
BC= ,
,∴OP=OB﹣BP=2﹣
 =
= ,
,此时满足条件的点P有一个,它是P4(0,
 ),
),综上所述,符合条件的点P有四个,
它们是:P1(0,2+

 )、P2(0,2﹣
)、P2(0,2﹣
 )、P3(0,
)、P3(0, )、P4(0,
)、P4(0, ).
).答:存在,所有满足条件的点P的坐标是P1(0,2+

 )、P2(0,2﹣
)、P2(0,2﹣
 )、P3(0,
)、P3(0, )、P4(0,
)、P4(0, ).
).
(1)把x=0,y=0分别代入解析式求出A、B的坐标,即可得出C、D的坐标;
(2)根据勾股定理求出CD,证△BMC∽△DOC,得到比例式即可求出答案;
(3)有两种情况:①以BM为腰时,满足BP=BM的有两个;过点M作ME⊥y轴于点E,证△BME∽△BCM,求出BE、PE,进一步求出OP即可;②以BM为底时,作BM的垂直平分线,分别交y轴、BM于点P、F,根据等腰三角形的性质求出即可.

练习册系列答案
相关题目
 (x>0)的图象交于点A(2,1),与x轴交于点B.
(x>0)的图象交于点A(2,1),与x轴交于点B.


 千克,付款金额
千克,付款金额 为元,则
为元,则
 的图象如图所示,则( )
的图象如图所示,则( )