题目内容
【题目】为响应市政府“创建国家森林城市”的号召,某小区计划购进A,B两种树苗共17棵,已知A种树苗每棵80元,B种树苗每棵60元。设购进A种树苗x棵,购买两种树苗的总费用为w元。
(1)写出w(元)关于x(棵)的函数关系式;
(2)若购买B种树苗的数量少于A种树苗的数量,请你给出一种费用最省的方案,并求出该方案所需费用。
【答案】(1)w=20x+1020;(2)费用最省方案为:购进A种树苗9棵,B种树苗8棵,所需费用为1200元.
【解析】
(1)根据题意可得等量关系:费用W=A种树苗a棵的费用+B种树苗(17a)棵的费用可得函数关系式;
(2)根据一次函数的性质与不等式的性质得到当x=9时,w有最小值.
解:(1)w= 80x+60(17-x) =20x+1020
(2) ∵k=20>0,w随着x的增大而增大
又∵17-x<x,解得x>8.5,
∴8.5<x<17,且x为整数
∴当x=9时,w有最小值20×9+1020=1200(元)
答:费用最省方案为:购进A种树苗9棵,B种树苗8棵,所需费用为1200元.

【题目】某校为了选拔学生参加区里“五好小公民”演讲比赛,对八年级一班、二班提前选好的各10名学生进行预选(满分10分),绘制成如下两幅统计表:
表(1):两班成绩
序号 | 1号 | 2号 | 3号 | 4号 | 5号 | 6号 | 7号 | 8号 | 9号 | 10号 |
一班(分) | 5 | 8 | 8 | 9 | 8 | 10 | 10 | 8 | 5 | 5 |
二班(分) | 10 | 6 | 6 | 9 | 10 | 4 | 5 | 7 | 10 | 8 |
表(2):两班成绩分析表
班级 | 平均分 | 中位数 | 众数 | 方差 | 及格率 |
一班 | 7.6 | a | b | 3.44 | 30% |
二班 | c | 7.5 | 10 | 4.45 | 40% |
(1)在表(2)中填空,a=________,b=________,c=________.
(2)一班、二班都说自己的成绩好,你赞同谁的说法?请给出两条理由.
【题目】甲,乙两班举行电脑汉字输入速度比赛,参赛学生每分钟输入汉字的个数经统计计算后,结果如下。 某同学根据上表分析,得出如下结论。
班级 | 参加人数 | 中位数 | 方差 | 平均数 |
甲 | 55 | 149 | 191 | 135 |
乙 | 55 | 151 | 110 | 135 |
(1)甲,乙两班学生成绩的平均水平相同。
(2)乙班优秀的人数多于甲班优秀的人数。(每分钟输入汉字≧150个为优秀。)
(3)甲班成绩的波动情况比乙班成绩的波动小。
上述结论中正确的是( )
A.(1) (2) (3)B.(1) (2)C.(1) (3)D.(2)(3)
【题目】(规律探究题)下表是按一定规律排列的一列方程,仔细观察,大胆猜想,科学推断,完成练习.
序号 | 方程 | 方程的解 |
1 | x2-2x-3=0 | x1=-1,x2=3 |
2 | x2-4x-12=0 | x1=-2,x2=6 |
3 | x2-6x-27=0 | x1=-3,x2=9 |
… | … | … |
(1)这列方程中第10个方程的两个根分别是x1=____,x2=____.
(2)这列方程中第n个方程为________.
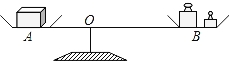
【题目】如图,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.实验数据记录如下表:
x(cm) | 10 | 15 | 20 | 25 | 30 |
y(g) | 30 | 20 | 15 | 12 | 10 |
(1)猜测y与x之间的函数关系,求出函数关系式并加以验证;
(2)当砝码的质量为24g时,活动托盘B与点O的距离是多少?
(3)将活动托盘B往左移动时,应往活动托盘B中添加还是减少砝码?