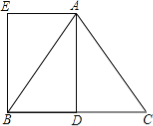题目内容
【题目】如图(1),在等边三角形![]() 中,
中,![]() 是
是![]() 边上的动点,以
边上的动点,以![]() 为一边,向上作等边三角形
为一边,向上作等边三角形![]() ,连接
,连接![]() .
.
(1)![]() 和
和![]() 全等吗?请说明理由;
全等吗?请说明理由;
(2)试说明:![]() ;
;
(3)如图(2),将动点![]() 运动到边
运动到边![]() 的延长线上,所作三角形
的延长线上,所作三角形![]() 仍为等边三角形,请问是否仍有
仍为等边三角形,请问是否仍有![]() ?请说明理由.
?请说明理由.

【答案】(1)![]() 和
和![]() 全等,理由见解析;(2)过程见解析;(3)仍有
全等,理由见解析;(2)过程见解析;(3)仍有![]() ,理由见解析.
,理由见解析.
【解析】
(1)要证两个三角形全等,已知的条件有:AC=BC,CE=CD,且∠BCD和∠ACE都是60°减去一个∠ACD,即可证明两个三角形全等;
(2)根据△DBC≌△EAC可得∠EAC=∠B=60°,又∠ACB=60°,所以∠EAC=∠ACB,即可得出结论;
(3)结合(1)(2)问的思路证明即可得出答案.
解:(1)![]() 和
和![]() 全等
全等
证明:∵△ABC和△DEC均为等边三角形
∴∠ACB=∠ECD=60°,BC=AC,CD=CE
又∠ACB=∠BCD+∠ACD
∠ECD=∠ECA+∠ACD
∴∠BCD=∠ECA
在△DBC和△EAC中
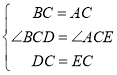
∴△DBC≌△EAC(SAS)
(2)∵△DBC≌△EAC
∴∠EAC=∠B=60°
又∠ACB=60°
∴∠EAC=∠ACB
∴AE∥BC
(3)仍有AE∥BC
理由:∵△ABC和△DEC均为等边三角形
∴∠ACB=∠ECD=60°,BC=AC,CD=CE
∴∠BCA+∠ACD=∠ACD+∠DCE
∴∠BCD=∠ACE
在△DBC和△EAC中
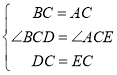
∴△DBC≌△EAC(SAS)
∴∠EAC=∠B=60°
又∠ACB=60°
∴∠EAC=∠ACB
∴AE∥BC

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目