Question

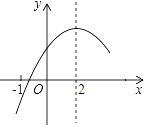
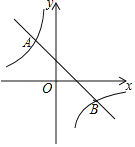
【题目】如图，一次函数y1＝kx+2图象与反比例函数y2＝图象相交于A，B两点，已知点B的坐标为(3，﹣1)．

（1）求一次函数和反比例函数的解析式；

（2）请直接写出不等式kx﹣≤﹣2的解集；

（3）点C为x轴上一动点，当S△ABC＝3时，求点C的坐标．

Answer 1

【答案】（1）y1＝﹣x+2，y2＝；（2）﹣1≤x＜0或x≥3；（3）(，0)或(，0)

【解析】

（1）将B的坐标（3，﹣1）分别代入一次函数y1＝kx+2图象与反比例函数y2＝中，可求出k、m的值，进而确定函数关系式，

（2）求出一次函数与反比例函数图象的交点坐标，根据图象得出不等式的解集，

（3）求出一次函数与x轴的交点坐标，根据S△ABC＝3，可以求出CM的长，分两种情况进行解答即可．

解：（1）把B（3，﹣1）分别代入y1＝kx+2和y2＝得：

﹣1＝3k+2，m＝3×（﹣1），

∴k＝﹣1，m＝﹣3，

∴一次函数和反比例函数的解析式分别为y1＝﹣x+2，y2＝，

（2）由题意得：

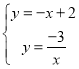，解得：，，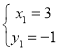

∴A（﹣1，3）

不等式kx﹣≤﹣2的解集，即kx+2≤的解集，由图象可得，﹣1≤x＜0或x≥3，

∴不等式kx﹣≤﹣2的解集为﹣1≤x＜0或x≥3．

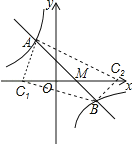
（3）直线y＝﹣x+2与x轴的交点M（2，0），即OM＝2，

∵S△ABC＝3，

∴S△AMC+S△BMC＝3

即：×CM×3+CM×1＝3，

解得：CM＝，

①当点C在M的左侧时，OC1＝2﹣＝，

∴点C的坐标为（，0），

②当点C在M的右侧时，OC2＝2+＝，

∴点C的坐标为（，0），

综合上述，点C的坐标为（，0）或（，0）．