题目内容
【题目】如图,△ABC,∠ABC、∠ACB的三等分线交于点E、D,若∠BFC=132°,∠BGC=120°,则∠E的度数为( ) 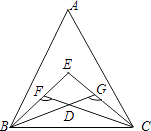
A.102°
B.104°
C.106°
D.108°
【答案】D
【解析】解:∵∠ABC、∠ACB的三等分线交于点E、D, ∴∠FBC=2∠DBC,∠GCB=2∠DCB,
∵∠BFC=132°,∠BGC=120°,
∴∠FBC+∠DCB=180°﹣∠BFC=180°﹣132°=48°,
∠DBC+∠GCB=180°﹣∠BGC=180°﹣120°=60°,
即 ![]() ,
,
由①+②可得:3(∠DBC+∠DCB)=108°,
∴∠EBC+∠ECB=2(∠DBC+∠DCB)=72°,
∴∠E=180°﹣(∠EBC+∠ECB)=180°﹣72°=108°,
故选D.
由三角形内角和及角平分线的定义可得到关于∠DBC和∠DCB的方程组,可求得∠DBC+∠DCB,则可求得∠EBC+∠ECB,再利用三角形内角和可求得∠E的度数.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目