题目内容
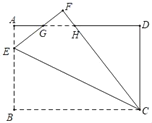
【题目】如图,在正方形ABCD中,E是CD上一点,连接AE.过点D作DM⊥AE,垂足为M,⊙O经过点A,B,M,与AD相交于点F.
(1)求证:△ABM∽△DFM;
(2)若正方形ABCD的边长为5,⊙O的直径为![]() ,求DE的长.
,求DE的长.
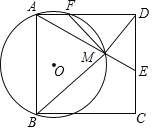
【答案】(1)见解析;(2) ![]()
【解析】
(1)由四边形ABCD为正方形,可得∠BAM=∠ADM,再由四边形BAFM为圆内接四边形,可得∠ABM=∠MFD,可以求证;
(2)连接BF,得BF为直径,由勾股定理可得到AF的长,从而得FD=3,因为△ABM∽△DFM,所以有![]() ,而易证△ADM∽△DEM,可得
,而易证△ADM∽△DEM,可得![]() ,即可得DE的长度.
,即可得DE的长度.
(1)证明:∵四边形ABCD为正方形,
∴∠BAD=90°,
∴∠BAM+∠MAF=90°,
∵DM⊥AE,
∴∠MAD+∠ADM=90°,
∴∠BAM=∠ADM,
∵四边形BAFM为圆内接四边形
∴∠ABM+∠AFM=180°
∴∠ABM=∠MFD
∴△ABM∽△DFM
(2)如图,连接BF,
∵∠BAF=90°,BF为直径
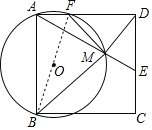
∴在Rt△ABF中,由勾股定理得AF=![]() =2,
=2,
∴FD=3,
∵△ABM∽△DFM,
∴![]() ,
,
∵∠DEM=∠ADM,∠AMD=∠DME=90°,
∴△ADM∽△DEM,
∴![]() ,
,
∴DE=![]() AD=
AD=![]() =
=![]()

【题目】某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动,每位同学必须且只能选择一项球类运动,对该校学生随机抽取![]() 进行调查,根据调查结果绘制了如图不完整的频数分布表和扇形统计图:
进行调查,根据调查结果绘制了如图不完整的频数分布表和扇形统计图:
运动项目 | 频数 |
羽毛球 | 30 |
篮球 | a |
乒乓球 | 36 |
排球 | b |
足球 | 12 |
请根据以上图表信息解答下列问题:
![]() 频数分布表中的
频数分布表中的![]() ______,
______,![]() ______;
______;
![]() 在扇形统计图中,“排球”所在的扇形的圆心角为______度;
在扇形统计图中,“排球”所在的扇形的圆心角为______度;
![]() 全校有多少名学生选择参加乒乓球运动?
全校有多少名学生选择参加乒乓球运动?

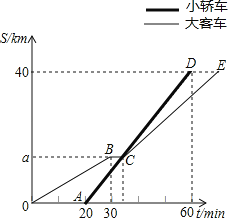
【题目】滴滴快车是一种便捷的出行工具,某地区计价规则如表:
计费项目 | 里程费 | 时长费 | 远途费 |
单价 | 1.8元/公里 | 0.3元/分钟 | 0.8元/公里 |
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程7公里以内(含7公里)不收远途费,超过7公里的,超出部分每公里收0.8元. | |||
小明与小亮各自乘坐滴滴快车,行车里程分别为6公里与8公里,如果下车时两人所付车费相同,那么这两辆滴滴快车的行车时间相差_____分钟.