题目内容
【题目】已知：在平面直角坐标系中，O为坐标原点，抛物线y＝ax2﹣2ax﹣3a分别交x轴于A、B两点（点A在点B的侧），与y轴交于点C，连接AC，tan∠ACO＝
．
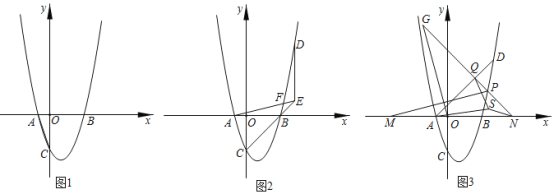
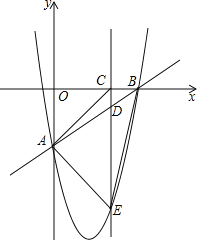
（1）如图l，求a的值；
（2）如图2，D是第一象限抛物线上的点，过点D作y轴的平行线交CB的延长线于点E，连接AE交BD于点F，AE＝BD，求点D的坐标；
（3）如图3，在（2）的条件下，连接AD，P是第一象限抛物线上的点（点P与点D不重合），过点P作AD的垂线，垂足为Q，交x轴于点N，点M在x轴上（点M在点N的左侧），点G在NP的延长线上，MP＝OG，∠MPN﹣∠MOG＝45°，MN＝10
．点S是△AQN内一点，连接AS、QS、NS，AS＝AQ，QS＝
SN，求QS的长．
【答案】(1) a=1; (2) D（4，5）;(3) 
【解析】
（1）由ax2-2ax-3a=0，可得到A（-1，0），B（3，0），OA=1，再根据条件tan∠ACO=
可求得C（0，-3），即可求出a的值；
（2）构造全等三角形Rt△ARE≌Rt△DRB，∴AR=DR，建立方程求解；
（3）过点G、P分别作x轴的垂线，垂足分别为K、H，构造全等三角形△MHP≌△GKO，利用特殊角45°构造等腰直角三角形，从而证得MK=HN=PH=KO，设点P（m，m2-2m-3），根据题目条件建立方程10
=m2-2m-3+m2-2m-3+m+m2-2m-3，可求得P（
，
）；过点A作AT⊥QS，垂足为T，过点N作NZ⊥QS，垂足为Z，构造全等三角形△ATQ≌△QZN，运用勾股定理可求出QS．
解：（1）如图1，
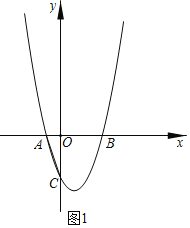
令y＝0，则ax2﹣2ax﹣3a＝0，
解得：x1＝﹣1，x2＝3，
∴A（﹣1，0），B（3，0），OA＝1，
∵tan∠ACO＝，∴OC＝3，即C（0，﹣3），
令x＝0，y＝﹣3a＝﹣3，∴a＝1
（2）如图2，延长DE交x轴于R，
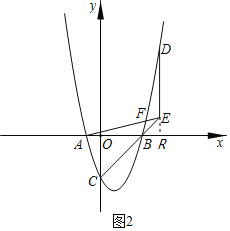
∵OC＝OB＝3，
∴∠OCB＝∠OBC＝45°，
∵DR∥y轴，
∴∠DER＝∠OCB＝45°，
∴∠RBE＝∠REB＝45°，
∴RB＝RE，
∵AE＝BD，
∴Rt△ARE≌Rt△DRB，
∴AR＝DR，
设D（t，t2﹣2t﹣3），AR＝t+1，DR＝t2﹣2t﹣3，
∴t+1＝t2﹣2t﹣3
解得：t1＝4，t2＝﹣1（舍去），
∴D（4，5）．
（3）如图3，过点G、P分别作x轴的垂线，垂足分别为K、H，
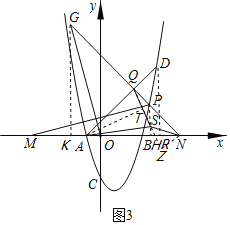
∵AR＝DR＝5，
∴∠RAD＝45°，
∵NG⊥AD，
∴∠AQN＝span>90°，
∴∠QAN＝∠QNA＝45°，
∵∠GKN＝90°，
∴∠KGN＝∠KNG＝45°，
∴GK＝KN，
∵∠PHN＝90°，
∴∠HPN＝∠HNP＝45°，
∴HP＝HN，
∵∠MPN﹣∠MOG＝45°，
∴∠MPH＝∠MOG，
∴∠MPH+∠HPN﹣∠MOG＝45°，
∵MP＝OG，∠MHP＝∠GKO＝90°，
∴△MHP≌△GKO，
∴MH＝GK，PH＝KO，
∵KN＝GK，
∴MH＝KN，
∴MK＝HN＝PH＝KO，
设点P（m，m2﹣2m﹣3），
∵MN＝MK+KO+OH+HN，
∴10＝m2﹣2m﹣3+m2﹣2m﹣3+m+m2﹣2m﹣3，
整理得：12m2﹣20m﹣77＝0，
解得：m1＝，m2＝-
（舍去），
∴P（，），
ON＝OH+HN＝
，AN＝AO+ON＝
，
在等腰直角三角形AQN中，由勾股定理可得QA＝QN＝
，
过点A作AT⊥QS，垂足为T，过点N作NZ⊥QS，垂足为Z，
∵∠QAT+∠AQT＝90°，∠NQZ+∠AQT＝90°，
∴∠QAT＝∠NQZ，
∵∠ATQ＝∠QZN＝90°，AQ＝NQ，
∴△ATQ≌△QZN（AAS），
∴QT＝ZN，AT＝QZ，
∵AQ＝AS，AT⊥QS，
∴QT＝ST，
即QT＝ZN＝ST＝
QS，
∵QS＝
SN，
∴2NZ═SN，sin∠ZSN＝
，
∴∠ZSN＝∠ZNS＝45°，
∴ZN＝ZS，
∴ZN＝ZS＝TS＝TQ＝AT，
在Rt△ATQ中，由勾股定理可得QT＝
∴QS＝2QT＝
．
